Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có: AB đường kính (gt), F ϵ (O)
⇒ △ BAF vuông tại F.
⇒ BF vuông góc với AF tại F. hay BF vuông góc với KF
Mà CD vuông góc với KF tại K (gt)
⇒ CD//BF
⇒ 2 cung nhỏ CF và BD chắn 2 dây // của (O) sẽ bằng nhau.
⇒ Đcpcm
b) Ta thấy CDBF là hình thang cân ( CD//BF, CF = BD )
⇒ 2 đường chéo BC = DF. (1)
Mà △ BCE cân tại B ( vì có BH vừa là đ/c, vừa là đường trung tuyến của △)
⇒BC=BE.(2)
Từ (1) và (2) ⇒ DF = BE.
⇒ cung DF = cung BE
Cộng 2 vế trên với cung EF ta đc:
cung DE = cung BF
⇒ DE = BF

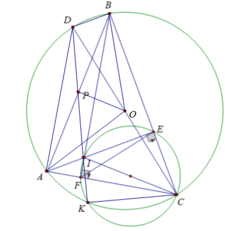
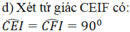
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.

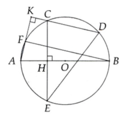
a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây

a: góc CTD=1/2*180=90 độ
góc CTF+góc COF=180 độ
=>CTFO nội tiếp
b: góc STF=1/2*sđ cung TD
góc SFT1/2(sđ cung AT+sđ cung BD)=1/2(sđ cung AT+sđ cung AD)=1/2*sđ cung TD
=>góc STF=góc SFT

.