Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

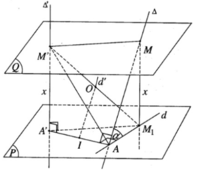
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.

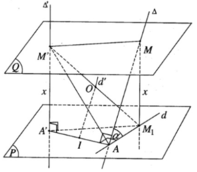
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
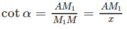
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên
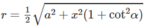

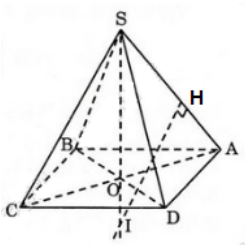
Qua O vẽ đường thẳng d vuông góc với (ABCD)
Khi đó d là trục đường tròn ngoại tiếp hình vuông ABCD
Gọi H là trung điểm của cạnh SA
Trong mặt phẳng (SAO) đường trung trực của đoạn SA cắt đường thẳng SO tại I , ta có: \(\Delta SAO\) đòng dạng \(\Delta SIH\)
\(\Rightarrow\dfrac{SA}{SO}=\dfrac{SI}{SH}\Leftrightarrow SI=\dfrac{SA.SH}{SO}=\dfrac{SA^2}{2SO}\)
Mà \(SA^2=SO^2+OA^2=\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=\dfrac{3a^2}{4}\)
\(\Leftrightarrow SA=\dfrac{a\sqrt{3}}{2}\)
Khi đó \(SI=\dfrac{3a^2}{\dfrac{4}{2.\dfrac{a}{2}}}=\dfrac{3a}{4}\)
Mặt khác \(\left\{{}\begin{matrix}IS=IA\\IA=IB=IC=ID\end{matrix}\right.\)
\(\Rightarrow IS=IA=IB=IC=ID=\dfrac{3a}{4}\)
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là I và bán kính \(R=SI=\dfrac{3a}{4}\)
Diện tích mặt cầu là: \(S=4\pi R^2=4\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{4}\)
Thể tích khối cầu là: \(V=\dfrac{4}{3}\pi R^2=\dfrac{4}{3}\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{16}\)


a) Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng \(\left(\alpha\right)\).
Theo giả thiết ta có \(\widehat{OAH}=30^0\)
Do đó : \(HA=OA\cos30^0=r\dfrac{\sqrt{3}}{2}\)


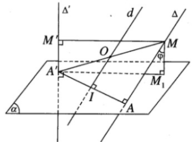
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

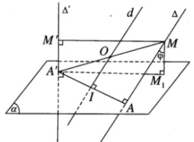
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
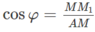
Do đó
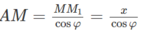
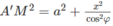
Mặt cầu tâm O có bán kính
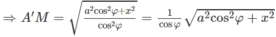
Diện tích của mặt cầu tâm O là:
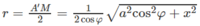


Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)