Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M thuộc Oy \(\Rightarrow M\left(0;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{BM}=\left(1;y-3\right)\end{matrix}\right.\)
ABM vuông tại B \(\Rightarrow\overrightarrow{AB}.\overrightarrow{BM}=0\)
\(\Rightarrow-2+y-3=0\Rightarrow y=5\)
\(\Rightarrow M\left(0;5\right)\)

Phương trình đường thẳng AB: \(4x+3y+12=0\)
Diện tích tam giác ABC nhỏ nhất khi khoảng cách từ điểm C đến AB nhỏ nhất.
\(d\left(C;AB\right)=\dfrac{\left|4.\dfrac{c^2}{4}+3c+12\right|}{5}=\dfrac{1}{5}.\left|\left(c+\dfrac{3}{2}\right)^2+\dfrac{39}{4}\right|\ge\dfrac{39}{20}\)
Dấu "=" xảy ra khi và chỉ khi \(c=-\dfrac{3}{2}\) => \(C\left(\dfrac{9}{16};-\dfrac{3}{2}\right)\)
❤Hana

Do M thuộc Ox, gọi tọa độ \(M\left(m;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;-2\right)\\\overrightarrow{MB}=\left(-m;1\right)\end{matrix}\right.\)
\(MA=MB\Leftrightarrow MA^2=MB^2\)
\(\Rightarrow\left(1-m\right)^2+\left(-2\right)^2=\left(-m\right)^2+1\)
\(\Leftrightarrow m^2-2m+1+4=m^2+1\Rightarrow m=2\)
\(\Rightarrow M\left(2;0\right)\)

\(\overrightarrow{AB}=\left(3;-3\right)\Rightarrow AB=3\sqrt{2}\)
\(S_{MAB}=\dfrac{1}{2}d\left(M;AB\right).AB=3\Rightarrow D\left(M;AB\right)=\dfrac{6}{AB}=\sqrt{2}\)
Phương trình AB:
\(1\left(x-0\right)+1\left(y-1\right)=0\Leftrightarrow x+y-1=0\)
\(M\in Oy\Rightarrow M\left(0;y\right)\Rightarrow d\left(M;AB\right)=\dfrac{\left|y-1\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
\(\Rightarrow\left|y-1\right|=2\Rightarrow\left[{}\begin{matrix}m=-1\\n=3\end{matrix}\right.\)

Đáp án C
+ Ta có: A B → = ( 3 ; 4 ) và AB= 5.
Do điểm M nằm trên trục tung nên tọa độ điểm M có dạng M(0; y)
+Khi đó diện tích tam giác MAB là S = 1 2 . A B . d ( M ; A B )
Thay số 1= 1/2.5.d( M; AB) nên d ( M ; A B ) = 2 5
+ Viết phương trình đường thẳng AB: đi qua A( 1; 2) và nhận A B → = ( 3 ; 4 ) làm VTCP nên nhận n → ( 4 ; - 3 ) làm VTPT.
Suy ra phương trình tổng quát: 4( x-1)- 3( y-2) =0
Hay 4x- 3y+ 2= 0
+ ta có:
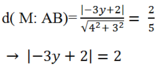
+ TH1: nếu -3y+ 2= 2 thì y= 0 và M( 0;0)
+ TH2: Nếu -3y+ 2= -2 thì y=4/3 và M( 0; 4/3).
Chọn A.
Hai điểm A(1;2) và B(4;6) ⇒ AB = 5
Gọi M(0;m).
Vì diện tích tam giác MAB bằng 1