Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a,`
`P(x)=M(x)+N(x)`
`P(x)=`\(\left(5x^4+8x^2-9x^3-12x-6\right)+\left(-5x^2+9x^3-5x^4+12x-8\right)\)
`P(x)= 5x^4+8x^2-9x^3-12x-6-5x^2+9x^3-5x^4+12x-8`
`P(x)=(5x^4-5x^4)+(-9x^3+9x^3)+(8x^2-5x^2)+(-12x+12x)+(-6-8)`
`P(x)=3x^2-14`
`b,`
`M(x)=N(x)+Q(x)`
`-> Q(x)=M(x)-N(x)`
`-> Q(x)=(5x^4+8x^2-9x^3-12x-6)-(-5x^2+9x^3-5x^4+12x-8)`
`Q(x)=5x^4+8x^2-9x^3-12x-6+5x^2-9x^3+5x^4-12x+8`
`Q(x)=(5x^4+5x^4)+(-9x^3-9x^3)+(8x^2+5x^2)+(-12x-12x)+(-6+8)`
`Q(x)=10x^4-18x^3+13x^2-24x+2`

Ta có p(x) + q(x)
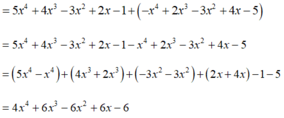
Bậc của đa thức p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 l à 4
Chọn đáp án C

`@` `\text {Ans}`
`\downarrow`
`a)`
`A(x) = \(3(x^2+2-4x)-2x(x-2)+17\)
`= 3x^2 + 6 - 12x - 2x^2 + 4x + 17`
`= x^2 - 8x + 23`
Hệ số cao nhất: `1`
Hệ số tự do: `23`
`B(x) = \(3x^2-7x+3-3(x^2-2x+4)\)
`=3x^2 - 7x + 3 - 3x^2 + 6x - 12`
`= -x - 9`
Hệ số cao nhất: `-1`
Hệ số tự do: `-9`
`b)`
`N(x) - B(x) = A(x)`
`=> N(x) = A(x) + B(x)`
`=> N(x) = (x^2 - 8x + 23)+(-x-9)`
`= x^2 - 8x + 23 - x - 9`
`= x^2 - 9x + 14`
`A(x) - M(x) = B(x)`
`=> M(x) = A(x) - B(x)`
`=> M(x) = (x^2 - 8x + 23) - (-x - 9)`
`= x^2 - 8x + 23 + x+9`
`= x^2 - 7x +32`
a)A(x) = 3(x^2 + 2 - 4x) - 2x(x - 2) + 17
= 3x^2 + 6 - 12x - 2x^2 + 4x + 17
= x^2 - 2x + 23
b)B(x) = 3x^2 - 7x + 3 - 3(x^2 - 2x + 4)
= 3x^2 - 7x + 3 - 3x^2 + 6x - 12
= -x + -9
A(x) = x^2 - 2x + 23
B(x) = -x - 9
Hệ số cao nhất của đa thức A(x) là 1, hệ số tự do của A(x) là 23.
Hệ số cao nhất của đa thức B(x) là -1, hệ số tự do của B(x) là -9.
b)
N(x) - B(x) = A(x)
N(x) - (-x - 9) = x^2 - 2x + 23
N(x) + x + 9 = x^2 - 2x + 23
N(x) = x^2 - 3x + 14
Vậy, N(x) = x^2 - 3x + 14.
A(x) - M(x) = B(x)
x^2 - 2x + 23 - M(x) = -x - 9
x^2 - 2x + x + 9 + 23 = M(x)
x^2 - x + 32 = M(x)
Vậy, M(x) = x^2 - x + 32.

b)
Sửa đề: f(x)=A(x)+B(x)
Ta có: f(x)=A(x)+B(x)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
a) Ta có: \(A\left(x\right)=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3+\left(-3x^2+x^2\right)-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Ta có: \(B\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+\left(x^2+3x^2\right)-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)

\(\cdot\) `\text {dnammv}`
`7,`
`a,`
`M(x)=\(-5x^4+3x^5+x\left(x^2+5\right)+14x^4-6x^5-x^3+x-1\)
`M(x)=-5x^4+3x^5+x^3+5x+14x^4-6x^5-x^3+x-1`
`=(3x^5-6x^5)+(-5x^4+14x^4)+(x^3-x^3)+(5x+x)-1`
`=-3x^5+9x^4+6x-1`
`N(x)=x^4(x - 5) - 3x^3 + 3x + 2x^5 - 4x^4 + 3x^3 - 5`
`= x^5-5x^4-3x^3+3x+2x^5-4x^4+3x^3-5`
`= 3x^5-9x^4+3x-5`
`b,`
`H(x)= N(x)+ M(x)`
`-> H(x)=(-3x^5+9x^4+6x-1)+(3x^5-9x^4+3x-5)`
`= -3x^5+9x^4+6x-1+3x^5-9x^4+3x-5`
`= (-3x^5+3x^5)+(9x^4-9x^4)+(6x+3x)+(-1-5)`
`= 9x-6`
`G(x)=M(x)-N(x)`
`-> G(x)= (-3x^5+9x^4+6x-1)-(3x^5-9x^4+3x-5)`
`= -3x^5+9x^4+6x-1-3x^5+9x^4-3x+5`
`= (-3x^5-3x^5)+(9x^4+9x^4)+(6x-3x)+(-1+5)`
`= -6x^5+18x^4+3x+4`
`c,`
`H(x)=9x-6`
Hệ số cao nhất: `9`
Hệ số tự do: `-6`
`G(x)= -6x^5+18x^4+3x+4`
Hệ số cao nhất: `-6`
Hệ số tự do: `4`
`d,`
`H(1)=9*1-6=9-6=3`
`H(-1)=9*(-1)-6=-9-6=-15`
`G(1)=-6*1^5+18*1^4+3*1+4=-6+18+3+4=12+3+4=15+4=19`
`G(0)=-6*0^5+18*0^4+3*0+4=0+0+0+4=4`
`H(x)=9x-6=0`
`-> 9x=0+6`
`-> 9x=6`
`-> x= 6 \div 9`
`-> x=`\(\dfrac{2}{3}\)
Vậy, nghiệm của đa thức là `x=`\(\dfrac{2}{3}\)

a)
\(A\left(x\right)=3x^3+3x^2+2x-1\)
Bậc của A(x) là 3
Hệ số tự do A(x) là -1
Hệ số cao nhất của A(x) là 3
Tại A(-2)
\(A=3.\left(-2\right)^3+3.\left(-2\right)^2+2.\left(-2\right)-1\)
\(=-17\)
b)
\(B\left(x\right)=5x^4+6x-2x^2+4-5x^4-5x\)
\(=\left(5x^4-5x^4\right)+\left(-2x^2\right)+\left(6x-5x\right)+4\)
\(=-2x^2+x+4\)
c)
\(A\left(x\right)-B\left(x\right)=3x^3+3x^2+2x-1-\left(-2x^2+x+4\right)\)
\(=3x^3+3x^2+2x-1+2x^2-x-4\)
\(=3x^3+\left(3x^2+2x^2\right)+\left(2x-x\right)+\left(-1-4\right)\)
\(=3x^3+5x^2+x-5\)
d)
\(C\left(x\right)-2.\left(-2x^2+x+4\right)=3x^3+3x^2+2x-1\)
\(C\left(x\right)=3x^3+3x^2+2x-1+2.\left(-2x^2+x+4\right)\)
\(C\left(x\right)=3x^3+3x^2+2x-1-4x^2+2x+8\)
\(C\left(x\right)=3x^3+\left(3x^2-4x^2\right)+\left(2x+2x\right)+\left(-1+8\right)\)
\(C\left(x\right)=3x^3-x^2+4x+7\)
chúc bạn học giỏi

a: \(M\left(x\right)=9x^4+2x^2-x-6\)
\(N\left(x\right)=-x^4-x^3-2x^2+4x+1\)
b: \(P\left(x\right)=8x^4-x^3+3x-5\)
\(Q\left(x\right)=10x^4+x^3+4x^2-5x-7\)
a: M(x)=5x^4+4x^3+2x+1-5x^4+x^3+3x^2+x-1
=5x^3+3x^2+3x
b: N(x)=5x^4+4x^3+2x+1+5x^4-x^3-3x^2-x+1
=10x^4+3x^3-3x^2+x+2
`@` `\text {dnammv}`
` \text {M(x)-A(x)=B(x)}`
`-> \text {M(x)=A(x)+B(x)}`
`-> M(x)=(5x^4 + 4x^3 + 2x + 1)+(-5x^4 + x^3 + 3x^2 + x - 1)`
`= 5x^4 + 4x^3 + 2x + 1-5x^4 + x^3 + 3x^2 + x - 1`
`= (5x^4-5x^4)+(4x^3+x^3)+3x^2+(2x+x)+(1-1)`
`= 5x^3+3x^2+3x`
`b,`
`\text {N(x)=A(x)-B(x)}`
`N(x)=(5x^4 + 4x^3 + 2x + 1)-(-5x^4 + x^3 + 3x^2 + x - 1)`
`= 5x^4 + 4x^3 + 2x + 1+5x^4 - x^3 - 3x^2 - x + 1`
`= (5x^4+5x^4)+(4x^3-x^3)-3x^2+(2x-x)+(1+1)`
`= 10x^4+3x^3-3x^2+x+2`