Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

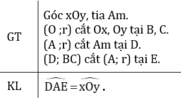
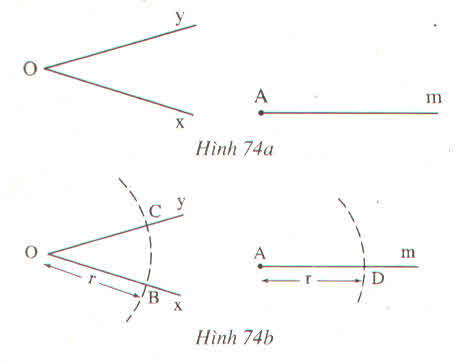
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
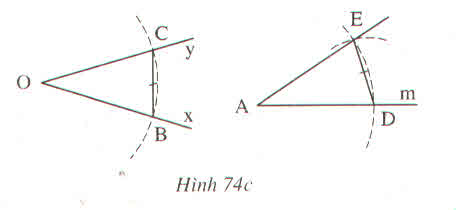
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
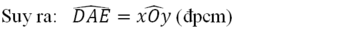

Xem hình bên rồi điền vào chỗ trồng (...) trong các câu sau:
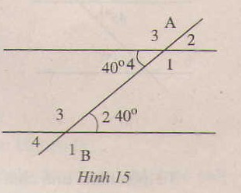
a) và
là một cặp góc .so le trong ....
b) và
là một cặp góc ..đồng vị ..
c) và
là một cặp góc ..đồng vị ....
d) và
là một ..cặp góc so le trong..
) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:

c) Ta có:
Bài 21 : a) Góc IPO và góc POR là 1 cặp góc so le trong
b) góc OPI và góc TNO là 1 cặp góc đồng vị
c) góc PIO và góc NTO là 1 cặp góc đồng vị
d)góc OPR và góc POI là một cặp góc so le trong

a) Ta có \(\widehat{BIK}\) là góc ngoài của \(\widehat{BAI}\)( hay là góc ngoài \(\widehat{BAK}\))
Các bạn lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên \(\widehat{BIK}>\widehat{BAK}\) (1)
b) Góc \(\widehat{CIK}>\widehat{CAI}\) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: \(\widehat{BIK}+\widehat{CIK}>\widehat{BAK}+\widehat{CAI}\)
Mà \(\widehat{BIC}=\widehat{BIK}+\widehat{CIK};\widehat{BAC}=\widehat{BAK}+\widehat{ CAI}\)
⇒ \(\widehat{BIC}>\widehat{BAC}\)
a, Ta có góc BIK là góc ngoài của Tg BAI
=> BIK=BAK+ABI
Mà ABI>0 => BIK>BAK
b, Tương tự CIK>CAK
=> BIK+CIK>BAK+CAK
=> BIC>BAC
Chúc bạn có một ngày mới tốt lành!

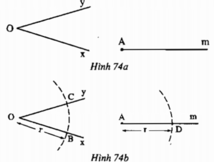
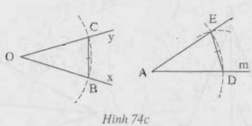
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra \(\widehat{DAE}\)=\(\widehat{BOC}\)(hai góc tương tứng)
vậy
\(\widehat{DAE}\)=\(\widehat{xOy}\).

Xét tam giác OBC và tam giác AED có
OB = AE (GT)
OC = AD (GT)
BC = ED (GT)
=> tam giác OBC = tam giác AED
=> góc xOy = góc DAE (2 góc tương ứng)
Vậy góc xOy = góc DAE

Xét tam giác OBC và tam giác AED có:
OB = AE (GT)
OC = AD (GT)
BC = ED (GT)
=> tam giác OBC = tam giác AED (c.c.c)
=> \(\widehat{xOy}\)=\(\widehat{DAE}\) (đpcm)