Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

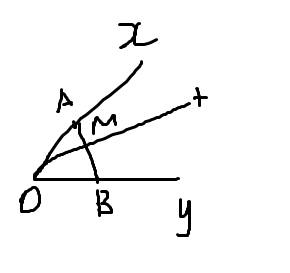
a. OA=OB
⇒ΔOAB cân tại O
mà OM là phân giác góc AOB
nên OM là đường trung tuyến ΔAOB
⇒M là trung điểm AB ⇒MA=MB
b. Xét ΔOAM và ΔOBM, có
OA=OB
OM chung
MA=MB
⇒ΔOAM = ΔOBM
nên OMA=OMB (đpcm)

Hình bạn tự vẽ nha
Xét \(\Delta AIO\) và \(\Delta BIO\) có:
OI chung
\(\widehat{AOI} = \widehat{BOI}\) (Oz là tia phân giác của \(\widehat{xOy}\) (gt))
OA = OB (gt)
\(\Rightarrow\)\(\Delta AIO = \Delta BIO\) (cgc)
b) Vì \(\Delta AIO = \Delta BIO\) (cmt)
\(\Rightarrow IB=IA\) (2 cạnh tương ứng)
mà OA = OB (gt)
\(\Rightarrow OI\) là đường trung trực của AB
hay \(AB \perp OI\)

cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a) Chứng minh: Góc BIM = Góc AIN
b) Chứng minh: MN // AB
M,N ở đâu ra

a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.g.c\right)\\ b,\text{Gọi }AB\cap OI=\left\{H\right\}\\ \left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOH=\Delta BOH\left(c.g.c\right)\\ \Rightarrow\widehat{AHO}=\widehat{BHO}\\ \text{Mà }\widehat{AHO}+\widehat{BHO}=180^0\\ \Rightarrow\widehat{AHO}=\widehat{BHO}=90^0\\ \Rightarrow OI\bot AB\)
Xét tg AOM và tg BOM có:
OA=OB (gt)
Góc AOM=góc BOM ( vì Oz là p/g của góc xOy )
Chung cạnh OM
=> Tg AOM = tg BOM ( c.g.c )
=> Góc OMA = góc OMB ( 2 góc tương ứng )
Còn đây là hình:( hơi tệ nên bạn thông cảm nha! )
A B M x y z O
Xet tam giac AOM va tam giac BOM la:
OA=OB (gt)
OM la canh chung
goc AOM= goc BOM (vi OZ la phan giac goc xOy)
Do do: tam giac OAM= tam giac OBM( c-g-c )
=> goc OMA = goc OMB (hai goc tuong ung)
O z y x B M A
Hinh hoi xau mog bn thog cam.