Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x O y A B C D M
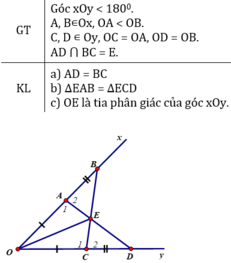
| GT | xOy ≠ 180o A, B C, D AD ∩ BC = { M } |
KL | a, AD = BC b, △MAB = △MCD |
Bài giải:
a, Xét △COB và △AOD
Có: OC = AC (gt)
xOy là góc chung
OB = OD (gt)
=> △COB = △AOD (c.g.c)
=> BC = AD (2 cạnh tương ứng)
b, Ta có: OB = AB + OA
OD = OC + CD
Mà OC = OA (gt) ; OD = OB (gt)
=> AB = CD
Vì △COB = △AOD (cmt)
=> CBO = ADO (2 góc tương ứng) và BCO = DAO (2 góc tương ứng)
Ta có: BAD + DAO = 180o (2 góc kề bù)
BCO + BCD = 180o (2 góc kề bù)
Mà BCO = DAO (cmt)
=> BAD = BCD
Xét △MAB và △MCD
Có: ABM = MDC (cmt)
AB = CD (cmt)
BAM = MCD (cmt)
=> △MAB = △MCD (g.c.g)

ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

a: Xét ΔOAD và ΔOCB có
OA=OC
góc AOD chung
OD=OB
=>ΔOAD=ΔOCB
=>AD=CB
b: Xét ΔEAB và ΔECD có
góc EAB=góc ECD
AB=CD
góc EBA=góc EDC
=>ΔEAB=ΔECD
c: Xét ΔOAE và ΔOCE có
OA=OC
AE=CE
OE chung
=>ΔOAE=ΔOCE
=>góc AOE=góc COE
=>góc AOM=góc CON
Xét ΔCON và ΔAOM có
góc CON=góc AOM
CO=AO
góc OCN=góc OAM
=>ΔCON=ΔAOM
=>ON=OM
=>ΔENM can tại E
=>EM=EN
=>NC=MA
Xét ΔEMB và ΔEND có
EM=EN
góc MEB=góc NED
EB=ED
=>ΔEMB=ΔEND
=>ND=MB và góc EMB=góc END
=>góc KMO=góc KNO
=>ΔKMN cân tại K
KD+DN=KN
KB+BM=KM
mà KM=KN; DN=BM
nên KD=KB
=>K nằm trên trung trực của DB(1)
OB=OD
nên O nằm trên trung trực của DB(2)
EB=ED
nên E nằm trên trung trực của DB(3)
Từ (1), (2), (3) suy ra O,E,K thẳng hàng

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB

Tam giác AOC có: AO = CO nên tam giác AOC cân tại O
⇒OAC=180−O2⇒OAC=180−O2
Tam giác BOD có OB = OD nên tam giác BOD cân tại O
⇒OBD=180−O2⇒OBD=180−O2
⇒OAC=OBD⇒OAC=OBDMà hai góc này ở vị trí đồng vị nên AC song song với BD.
 Ox: OA < OB
Ox: OA < OB
Xét tam giác OBC và tam giác ODA,có:
OB=OD ( giả thiết )
\(\widehat{o}\):chung
OA=OC ( giả thiết )
=>tam giác OBC = tam giác ODA (c-g-c)
=>\(\widehat{OBC}=\widehat{ODA}\)(2 góc tương ứng)
Ta có :OA+AB=OB
OC+CD=OD
Mà \(\hept{\begin{cases}OA=OC\\OB=OD\end{cases}=>AB=CD}\)
Mặt khác,có: \(\widehat{AMB}=\widehat{ABM}\)(2 góc đối đỉnh)
\(\widehat{ABM}=\widehat{CDM}\)(Chứng minh trên)
=>\(\widehat{MAB}=\widehat{MCD}\)
Xét tam giác ABM và tam giác CDM,có:
\(\widehat{MAB}=\widehat{MCD}\)(Chứng minh trên)
AB=CD(Chứng minh trên )
\(\widehat{ABM}=\widehat{MCD}\)(Chứng minh trên )
=> tam giác ABM = tam giác CDM(g-c-g)
=>BM=MD (2 cạnh tương ứng)
Xét tam giác MBO và tam giác MDO,có:
OB=OD(Gt)
\(\widehat{ODM}=\widehat{MBO}\)(Chứng minh trên)
BM=MD(Chứng minh trên)
=>tam giác MBO = tam giác MDO(c-g-c)
=>\(\widehat{xOm}=\widehat{yOm}\)(2 góc tương ứng)
=>\(\widehat{xOm}\)=\(\frac{1}{2}\)\(\widehat{xOy}\)=700