Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải
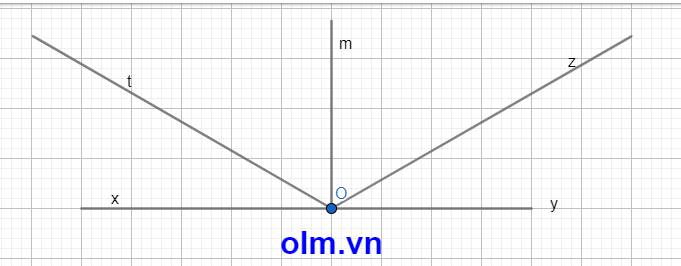
x y z O t m
Vì \(\widehat{xOz}=\widehat{yOt}=150^o\) có \(\widehat{tOz}\) chung \(\widehat{tOx}=\widehat{yOz}\) mà \(\widehat{yOz}=\widehat{yOm}\left(=\frac{1}{2}\widehat{mOz}\right)\)
\(\Rightarrow\text{ }\widehat{xOt}=\widehat{yOm}\)
Ta dễ dàng chứng minh được \(Om\) và \(Ot\) đối nhau
\(\Rightarrow\text{ }\widehat{tOy}\text{ và }\widehat{mOx}\) là hai góc đối nhau

A) Nếu tia OC nằm giữa hai tia OA và OA' thì:\
AOC+COA'=AOA'
=> 90 + COA' = AOA'
mà AOA' là góc kề bù nên AOA'=180 độ
=> 90+ COA' = 180độ
=> COA= 180 -90
=>COA=90 độ
Vì tia OB' là tia phân giác của góc COA' nên :
B'OA' = 90:2
=> B'OA' =45
Hai góc AOB và OB'A' là hai góc đối đỉnh vì AOB=OB'A'( hay 45 =45)
BÀI 1
b) Vì tia OB nằm giữa hai tia OD và OA nên:
AOB + BOD=ADO
=> 45 + 90 = AOD
=> AOD=135 độ
Vì tia OD nằm giữa hai tia OA và OA' nên:
AOD+DOA'=AOA'
=> 135+DOA'=AOA'
mà AOA' là góc kề bù nên AOA' = 180 độ
=> 135+ DOA'= 180 độ
=> DOA'=180 độ -135 độ
=> DOA'=45 độ

bạn mở bài định lí sgk toán 7 tập 1 , có CM 2 tia pg của 2 góc kề bù tạo vs nhau thành góc vuông. Bài trên ngược lại vs bài trong sách

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a,
\(\widehat{tOz}\) + \(\widehat{xOt}\) + \(\widehat{yOz}\) =1800
⇒\(\widehat{tOz}\) = 1800 - ( \(\widehat{xOt}\) + \(\widehat{yOz}\))
\(\widehat{tOz}\) = 1800 - (300 + 300) = 1200
b, Om là phân giác của góc \(x\)Oy vì:
\(\widehat{mOt}\) = \(\widehat{mOz}\) = \(\dfrac{1}{2}\) \(\widehat{xOz}\) (vì Om là phân giác của góc tOz)
⇒ \(\widehat{mOt}\) = \(\widehat{mOz}\) = 1200 : 2 = 600
\(\widehat{xOm}\) = \(\widehat{xOt}\) + \(mOt\) = 300 + 600 = 900
\(\widehat{mOy}\) = \(\widehat{mOz}\) + \(\widehat{yOz}\) = 300 + 600 = 900
⇒ \(\widehat{xOm}\) = \(\widehat{mOy}\) mà Om nằm giữa hai tia \(Ox\) và Oy
Nên Om là tia phân giác của góc \(x\)Oy