Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề là cho \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx=1\)
Tính \(\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx\)
Đúng ko nhỉ?
Xét \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx\)
Đặt \(cos^2x=1-u\Rightarrow-2sinx.cosxdx=-du\) \(\Rightarrow sin2xdx=du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=\dfrac{\pi}{2}\Rightarrow u=1\end{matrix}\right.\) \(\Rightarrow I=\int\limits^1_0f\left(1-u\right)du=\int\limits^1_0f\left(1-x\right)dx\)
\(\Rightarrow\int\limits^1_0f\left(1-x\right)dx=1\)
\(\Rightarrow\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx=2\int\limits^1_0f\left(1-x\right)dx-\int\limits^1_0\left(3x^2-5\right)dx\)
\(=2.1-\left(-4\right)=6\)

Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
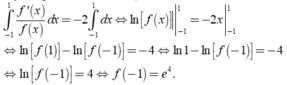

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.

\(f\left(0\right)=-1\Rightarrow f'\left(0\right)+2=0\Leftrightarrow f'\left(0\right)=-2\)
\(\int\limits^1_0f\left(x\right)dx=\int\limits^1_0\dfrac{f'\left(x\right)-x.e^{3x}}{2}dx=\dfrac{1}{2}\int\limits^1_0f'\left(x\right)dx-\dfrac{1}{2}\int\limits^1_0x.e^{3x}dx=\dfrac{1}{2}f\left(x\right)|^1_0-\dfrac{1}{2}\int\limits^1_0xe^{3x}dx\)
\(I_1=\int xe^{3x}dx\)
\(\left\{{}\begin{matrix}u=x\\dv=e^{3x}dx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=dx\\v=\dfrac{1}{3}e^{3x}\end{matrix}\right.\)
\(\Rightarrow I_1=\dfrac{1}{3}xe^{3x}-\dfrac{1}{3}\int e^{3x}dx=\dfrac{1}{3}xe^{3x}-\dfrac{1}{9}e^{3x}\)
\(\Rightarrow I=\dfrac{1}{2}f\left(1\right)-\dfrac{1}{2}f\left(0\right)-\dfrac{1}{2}\left(\dfrac{1}{3}xe^{3x}-\dfrac{1}{9}e^{3x}\right)|^1_0\)
Èo, tắc chỗ f(1) rồi, vậy đành phải biến đổi để tìm f(x) luôn vậy, hmm
Thử nhân 2 vế với \(e^{2x}\) xem nào:
\(e^{2x}f'\left(x\right)-2e^{2x}f\left(x\right)=x.e^{5x}\Leftrightarrow\left(e^{2x}.f\left(x\right)\right)'=x.e^{5x}\)
Lay nguyen ham 2 ve:
\(e^{2x}.f\left(x\right)=\int x.e^{5x}dx\)
\(\left\{{}\begin{matrix}x=u\\dv=e^{5x}dx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}dx=du\\v=\dfrac{1}{5}e^{5x}\end{matrix}\right.\)
\(\Rightarrow e^{2x}.f\left(x\right)=\int x.e^{5x}dx=\dfrac{1}{5}x.e^{5x}-\dfrac{1}{5}\int e^{5x}dx=\dfrac{1}{5}xe^{5x}-\dfrac{1}{25}e^{5x}+C\)
\(f\left(0\right)=-1\Leftrightarrow f\left(0\right)=-\dfrac{1}{25}+C=-1\Leftrightarrow C=-\dfrac{24}{25}\)
\(\Rightarrow f\left(x\right)=\dfrac{\dfrac{1}{5}xe^{5x}-\dfrac{1}{25}e^{5x}-\dfrac{24}{25}}{e^{2x}}\)
Vậy là xong rồi \(\Rightarrow f\left(1\right)=...\) , thay vô \(I=\dfrac{1}{2}f\left(1\right)-\dfrac{1}{2}.\left(-1\right)-\dfrac{1}{2}\left(\dfrac{1}{3}xe^{3x}-\dfrac{1}{9}e^{3x}\right)|^1_0\) là được nha :)
Nguyên tắc:
\(g\left(x\right).f'\left(x\right)+h\left(x\right).f\left(x\right)=p\left(x\right)\)
Đầu tiên luôn biến đổi để \(f'\left(x\right)\) đứng riêng biệt 1 mình:
\(\Rightarrow f'\left(x\right)+\dfrac{h\left(x\right)}{g\left(x\right)}.f\left(x\right)=\dfrac{p\left(x\right)}{g\left(x\right)}\) (1)
Cần thêm/bớt, nhân/chia sao cho biến về dạng:
\(\left[u\left(x\right).f\left(x\right)\right]'=q\left(x\right)\)
\(\Leftrightarrow f'\left(x\right).u\left(x\right)+u'\left(x\right).f\left(x\right)=q\left(x\right)\)
\(\Leftrightarrow f'\left(x\right)+\dfrac{u'\left(x\right)}{u\left(x\right)}.f\left(x\right)=\dfrac{q\left(x\right)}{u\left(x\right)}\)
Chỉ quan tâm vế trái, khi đó ta sẽ thấy hàm đằng trước \(f\left(x\right)\) chính là \(\dfrac{u'\left(x\right)}{u\left(x\right)}\)
Đồng nhất \(\Rightarrow\dfrac{u'\left(x\right)}{u\left(x\right)}=-2\)
Lấy nguyên hàm 2 vế \(\Rightarrow ln\left|u\left(x\right)\right|=-2x\Rightarrow u\left(x\right)=e^{-2x}\)
Do đó, ở bài toán ban đầu ta cần nhân 2 vế của (1) với \(u\left(x\right)=e^{-2x}\) nghĩa là:
\(f'\left(x\right)-2f\left(x\right)=x.e^{3x}\Leftrightarrow e^{-2x}.f'\left(x\right)-2e^{-2x}.f\left(x\right)=x.e^x\)
\(\Leftrightarrow\left[e^{-2x}.f\left(x\right)\right]'=x.e^x\)
Nguyên hàm 2 vế: \(\Rightarrow e^{-2x}.f\left(x\right)=\left(x-1\right)e^x+C\)
Thay \(x=0\Rightarrow1.f\left(0\right)=-1+C\Rightarrow C=0\)
\(\Rightarrow e^{-2x}.f\left(x\right)=\left(x-1\right)e^x\Rightarrow f\left(x\right)=\left(x-1\right)e^{3x}\)
\(\Rightarrow I=\int\limits^1_0\left(x-1\right)e^{3x}dx=...\)

Lời giải:
Ta có:\(F(x)=\int (2x-3)\ln xdx\)
Đặt \(\left\{\begin{matrix} u=\ln x\\ dv=(2x-3)dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dx}{x}\\ v=\int (2x-3)dx=x^2-3x\end{matrix}\right.\)
Do đó:
\(F(x)=\int (2x-3)\ln xdx=(x^2-3x)\ln x-\int (x^2-3x).\frac{dx}{x}\)
\(=(x^2-3x)\ln x-\int (x-3)dx=(x^2-3x)\ln x-(\frac{x^2}{2}-3x)+c\)
Với \(x=1\)
\(F(1)=\frac{5}{2}+c=0\Rightarrow c=\frac{-5}{2}\)
Vậy \(F(x)=(x^2-3x)\ln x-\frac{x^2}{2}+3x-\frac{5}{2}\)
\(\Rightarrow 2F(x)+x^2-6x+5=2(x^2-3x)\ln x-x^2+6x-5+x^2-6x+5\)
\(=2(x^2-3x)\ln x=0\)
\(\Leftrightarrow \left[\begin{matrix} x=0\\ x=3\\ x=1\end{matrix}\right.\)
Tức là pt có 3 nghiệm.
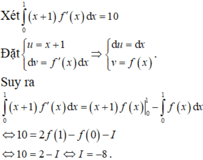
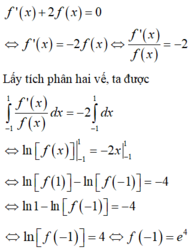
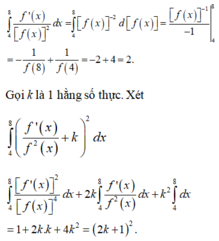
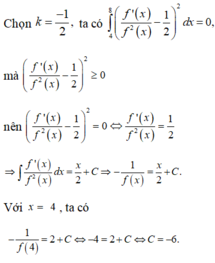
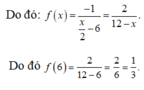
\(f\left(x\right)+2f'\left(x\right)+f''\left(x\right)=x^3+2x^2\)
\(\Leftrightarrow f\left(x\right)+f'\left(x\right)+f'\left(x\right)+f''\left(x\right)=x^3+2x^2\)
\(\Leftrightarrow f\left(x\right)+f'\left(x\right)+\left[f\left(x\right)+f'\left(x\right)\right]'=x^3+2x^2\)
Đặt \(f\left(x\right)+f'\left(x\right)=u\left(x\right)\) ta được:
\(u\left(x\right)+u'\left(x\right)=x^3+2x^2\)
\(\Leftrightarrow e^x.u\left(x\right)+e^x.u'\left(x\right)=e^x\left(x^3+2x^2\right)\)
\(\Leftrightarrow\left[e^x.u\left(x\right)\right]'=e^x\left(x^3+2x^2\right)\)
\(\Rightarrow e^x.u\left(x\right)=\int e^x\left(x^3+2x^2\right)dx=e^x\left(x^3-x^2+2x-2\right)+C\)
\(\Leftrightarrow e^x\left[f\left(x\right)+f'\left(x\right)\right]=e^x\left(x^3-x^2+2x-2\right)+C\)
Thay \(x=0\) vào ta được \(2=-2+C\Rightarrow C=4\)
\(\Rightarrow e^x.f\left(x\right)+e^x.f'\left(x\right)=e^x\left(x^3-x^2+2x-2\right)+4\)
\(\Leftrightarrow\left[e^x.f\left(x\right)\right]'=e^x\left(x^3-x^2+2x-2\right)+4\)
\(\Rightarrow e^x.f\left(x\right)=\int\left[e^x\left(x^3-x^2+2x-2\right)+4\right]dx\)
\(\Rightarrow e^x.f\left(x\right)=e^x\left(x^3-4x^2+10x-12\right)+4x+C_1\)
Thay \(x=0\) vào ta được: \(1=-12+C_1\Rightarrow C_1=13\)
\(\Rightarrow e^x.f\left(x\right)=e^x\left(x^3-4x^2+10x-12\right)+4x+13\)
\(\Rightarrow f\left(x\right)=x^3-4x^2+10x-12+\frac{4x+13}{e^x}\)
\(\Rightarrow\int\limits^1_0f\left(x\right)dx=\int\limits^1_0\left(x^3-4x^2+10x-12\right)dx+\int\limits^1_0\left(4x+13\right).e^{-x}dx\)
Tích phân trước bạn tự tính, tích phân sau cũng đơn giản thôi:
Đặt \(\left\{{}\begin{matrix}u=4x+13\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=4dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I=-\left(4x+13\right).e^{-x}|^1_0+4\int\limits^1_0e^{-x}dx=\frac{-17}{e}+13-4.e^{-x}|^1_0=17-\frac{21}{e}\)
Casio cho kết quả tích phân trước là \(-\frac{97}{12}\)
Vậy \(\int\limits^1_0f\left(x\right)dx=\frac{107}{12}-\frac{21}{e}\)