Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Hình vẽ câu 1) đúng
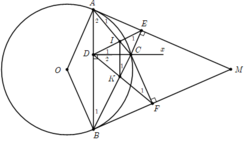
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

O B A C M N P Q I K
a) Do AMNP là hình vuông nên \(\widehat{QMB}=45^o\)
Lại có do C là điểm chính giữa của nửa đường tròn nên \(\widebat{CB}=90^o\Rightarrow\widehat{CMB}=45^o\)
(Góc nội tiếp)
Vậy thì \(\widehat{CMQ}=\widehat{CMB}+\widehat{BMQ}=45^o+45^o=90^o\)
Vậy CQ là đường kính hay C và Q đối xứng nhau qua O.
b) Ta thấyAMNP là hình vuông. MI là phân giác góc \(\widehat{AMB}\) nên \(\Delta MAI=\Delta MNI\left(c-g-c\right)\Rightarrow\widehat{MAI}=\widehat{MNI}\)
Lại có \(\widehat{MAI}=\widehat{IAM}\) nên \(\widehat{MNI}=\widehat{IAM}\)
Xét tứ giác AINB có \(\widehat{MNI}=\widehat{IAM}\) nên AINB là tứ giác nội tiếp (góc ngoài tại đỉnh bằng góc đối diện)