Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là giao điểm của AH và EF
Tứ giác AEHF là hình chữ nhật => AH = EF
Do đó EF là tiếp tuyến của đường tròn (I)
Tương tự, EF là tiếp tuyến của đường tròn (K)

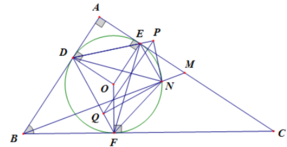
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

O A B x y C C E F D I H K
a, Theo t/c tiếp tuyến của đường tròn
EA = EC
FC = FB
=> EC + CF = EA + BF
=> EF = AE + BF
b, Xét \(\Delta\)ABC có OA = OB = OC (bán kính)
=> \(\Delta\)ABC vuông tại C
=> AC \(\perp\)BC
Xét \(\Delta\)DAB vuông tại A có AC là đường cao
=> \(AD^2=DC.DB\)(Hệ thức lượng)
c,Chưa ra, mai nghĩ ra thì giải cho ^^