Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tiếp tuyến tại A và B của (O) cắt nhau tại C.CM cắt (I) tại N'
Xét \(\Delta CAM\) và \(\Delta CN'A:\) Ta có: \(\left\{{}\begin{matrix}\angle ACN'chung\\\angle CAM=\angle CN'A\end{matrix}\right.\)
\(\Rightarrow\Delta CAM\sim\Delta CN'A\left(g-g\right)\Rightarrow\dfrac{CA}{CN'}=\dfrac{CM}{CA}\Rightarrow CA^2=CM.CN'\)
mà \(CA^2=CB^2\Rightarrow CB^2=CM.CN'\Rightarrow\dfrac{CB}{CM}=\dfrac{CN'}{CB}\)
Xét \(\Delta CBM\) và \(\Delta CN'B:\) Ta có: \(\left\{{}\begin{matrix}\angle BCN'chung\\\dfrac{CB}{CM}=\dfrac{CN'}{CB}\end{matrix}\right.\)
\(\Rightarrow\Delta CBM\sim\Delta CN'B\left(c-g-c\right)\Rightarrow\angle CBB=\angle CN'B\Rightarrow N'\in\left(J\right)\)
\(\Rightarrow N\equiv N'\Rightarrow MN\) luôn đi qua điểm C mà A,B cố định
\(\Rightarrow C\) cố định \(\Rightarrow\) đpcm
b) mình chỉ chứng minh được N thuộc 1 đường tròn cố định thôi,còn chạy trên đoạn thẳng hình như là ko được
Ta có: \(\angle ANB=\angle ANM+\angle BNM=\dfrac{1}{2}\angle AIM+\dfrac{1}{2}\angle BJM\)
Xét \(\Delta AIM\) và \(\Delta AOB:\) Ta có: \(\left\{{}\begin{matrix}\angle OABchung\\\dfrac{IA}{OA}=\dfrac{IM}{OB}\end{matrix}\right.\)
\(\Rightarrow\Delta AIM\sim\Delta AOB\left(c-g-c\right)\Rightarrow\angle AIM=\angle AOB\)
Tương tự \(\Rightarrow\angle BJM=\angle AOB\)
\(\Rightarrow\angle ANB=\dfrac{1}{2}\angle AOB+\dfrac{1}{2}\angle AOB=\angle AOB\)
\(\Rightarrow N\in\left(AOB\right)\) mà A,O,B cố định \(\Rightarrow N\in\left(AOB\right)\) cố định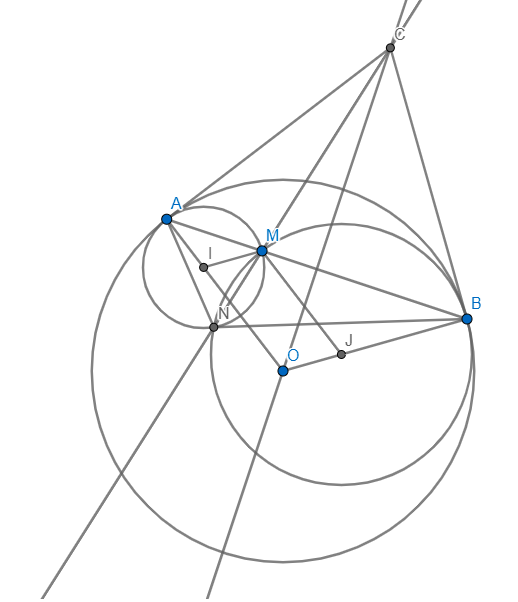
hình :
O' O M N A B C
lời giải :
a) MN cắt ( O ) tại C
dễ thấy O'N vuông góc với AB
Ta có : \(\Delta O'MN\)cân tại O' nên \(\widehat{O'MN}=\widehat{O'NM}\)( 1 )
Mà \(\Delta OMC\)cân tại O nên \(\widehat{OMC}=\widehat{OCM}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{O'NM}=\widehat{OCM}\)nên O'N // OC
\(\Rightarrow OC\perp AB\), suy ra C cố định
b) vẽ bán kính \(OC\perp AB\) ( C và M thuộc hai nửa mặt phẳng đối nhau bờ AB )
CM cắt AB tại N
đường thẳng qua N và song song với OC cắt OM tại O'
Dựng đường tròn ( O';O'M )
đó là đường tròn phải dựng