Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D M A J C O J B
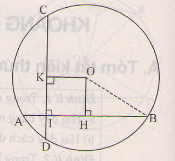
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra : J là trung điểm của AB
Ta được : \(AJ=\frac{1}{2}AB=4cm\)
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 ( OA = R = 5cm )
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có :\(\widehat{I}=\widehat{J}=\widehat{M}=90^o\)nên là hcn
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

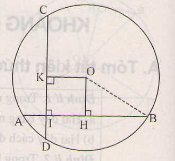
a) Vẽ OH⊥ABOH⊥AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2=OB2−HB2=52−42=9⇒OH=3(cm)OH2=OB2−HB2=52−42=9⇒OH=3(cm).
b) Vẽ OK⊥CDOK⊥CD. TỨ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI. Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm.
Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
a) Vẽ OH ⊥ AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2 = OB2 – HB2 =52 – 42 = 9
⇒ OH = 3(cm).
b) Vẽ OK ⊥ CD. Tứ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI.
Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm. Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.

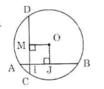
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
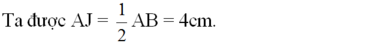
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
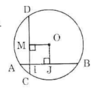
Tứ giác OJIM có: 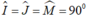 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

Lời giải chi tiết
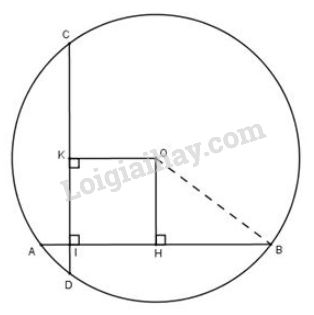
a) Kẻ OH⊥ABOH⊥AB tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra HH là trung điểm của dây ABAB (Theo định lí 2 - trang 103)
⇒HA=HB=AB2=82=4cm.⇒HA=HB=AB2=82=4cm.
Xét tam giác HOBHOB vuông tại HH, theo định lí Pytago, ta có:
OB2=OH2+HB2⇔OH2=OB2−HB2OB2=OH2+HB2⇔OH2=OB2−HB2
⇔OH2=52−42=25−16=9⇒OH=3(cm)⇔OH2=52−42=25−16=9⇒OH=3(cm).
Vậy khoảng cách từ tâm OO đến dây ABAB là 3cm3cm.
b) Vẽ OK⊥CDOK⊥CD tại K
Tứ giác KOHIKOHI có ba góc vuông (ˆK=ˆH=ˆI=900)(K^=H^=I^=900) nên là hình chữ nhật, suy ra OK=HIOK=HI.
Ta có HI=AH−AI=4−1=3cmHI=AH−AI=4−1=3cm, suy ra OK=3cm.OK=3cm.
Vậy OH=OK=3cm.OH=OK=3cm.
Hai dây ABAB và CDCD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
Lời giải chi tiết

a) Kẻ OH⊥ABOH⊥AB tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra HH là trung điểm của dây ABAB (Theo định lí 2 - trang 103)
⇒HA=HB=AB2=82=4cm.⇒HA=HB=AB2=82=4cm.
Xét tam giác HOBHOB vuông tại HH, theo định lí Pytago, ta có:
OB2=OH2+HB2⇔OH2=OB2−HB2OB2=OH2+HB2⇔OH2=OB2−HB2
⇔OH2=52−42=25−16=9⇒OH=3(cm)⇔OH2=52−42=25−16=9⇒OH=3(cm).
Vậy khoảng cách từ tâm OO đến dây ABAB là 3cm3cm.
b) Vẽ OK⊥CDOK⊥CD tại K
Tứ giác KOHIKOHI có ba góc vuông (ˆK=ˆH=ˆI=900)(K^=H^=I^=900) nên là hình chữ nhật, suy ra OK=HIOK=HI.
Ta có HI=AH−AI=4−1=3cmHI=AH−AI=4−1=3cm, suy ra OK=3cm.OK=3cm.
Vậy OH=OK=3cm.OH=OK=3cm.
Hai dây ABAB và CDCD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
* Mạng :))) *
#Ninh Nguyễn

Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: 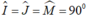 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

a.Gọi MM là trung điểm AB → OM ⊥ AB, MA = MB = 1/2AB = 4
→OA2=OM2+MA2
→OM2=OA2−MA2=9
→OM=3
→Khoảng cách từ tâm O đến AB bằng 3cm
b.Ta có AI = 1 → IM = MA − MI = 3
Gọi OE ⊥ CD = E
Vì OM ⊥ AB, CD ⊥ AB = I
→OEIM là hình chữ nhật
→OE = IM = 3 → OE = OM vì OM = 3
→d (O,CD) = d (O,AB)
→CD=AB
a: Gọi OM là khoảng cách từ O đến AB
Suy ra: M là trung điểm của AB
hay \(AM=BM=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOMA vuông tại M, ta được:
\(OA^2=OM^2+MA^2\)
\(\Leftrightarrow OM^2=5^2-4^2=9\)
hay OM=3(cm)
c