Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

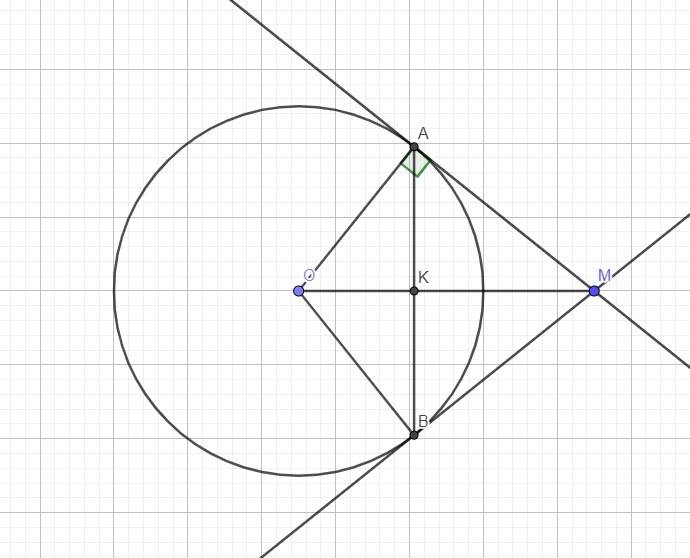
Xét đường tròn (O;R) có A, B \(\in\left(O;R\right)\)\(\Rightarrow OA=OB=R\)
Mà \(R=3cm\left(gt\right)\Rightarrow OA=OB=3cm\)
Vì MA là tiếp tuyến tại A của (O) (gt) \(\Rightarrow MA\perp OA\)tại A \(\Rightarrow\Delta OMA\)vuông tại A
\(\Rightarrow OM^2=OA^2+AM^2\left(đlPytago\right)\)\(\Rightarrow AM^2=OM^2-OA^2\Rightarrow AM=\sqrt{OM^2-OA^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4\left(cm\right)\)
Xét đường tròn (O) có hai tiếp tuyến tai A và B cắt nhau tại M (gt) \(\Rightarrow MA=MB\)(tính chất hai tiếp tuyến cắt nhau)
Mà \(MA=4cm\left(cmt\right)\Rightarrow MB=4cm\)
Chu vi tứ giác AMBO là \(MA+MB+OA+OB=4+4+3+3=14\left(cm\right)\)
Gọi H là giao điểm của OM và AB.
Ta có \(MA=MB\left(cmt\right)\)\(\Rightarrow\)M nằm trên đường trung trực của AB. (1)
Lại có \(OA=OB\left(=R\right)\)\(\Rightarrow\)O nằm trên đường trung trực của AB. (2)
Từ (1) và (2) \(\Rightarrow\)OM lả đường trung trực của AB. \(\Rightarrow\hept{\begin{cases}AH=BH=\frac{AB}{2}\\AH\perp OM\left(H\in OM\right)\end{cases}}\)
\(\Rightarrow\)AH là đường cao của \(\Delta OMA\)
Xét \(\Delta OMA\)vuông tại A có đường cao AH (cmt) \(\Rightarrow AH.OM=MA.OA\left(htl\right)\)
\(\Rightarrow AH=\frac{MA.OA}{OM}=\frac{4.3}{5}=\frac{12}{5}=2,4\left(cm\right)\)
\(\Rightarrow AB=2AH=2.2,4=4,8\left(cm\right)\)
Xét tiếp \(\Delta OMA\)vuông tại A có đường cao AH \(\Rightarrow MA^2=MH.MO\left(htl\right)\)
\(\Rightarrow MH=\frac{MA^2}{MO}=\frac{4^2}{5}=\frac{16}{5}=3,2\left(cm\right)\)
Diện tích \(\Delta MAB\)là \(S_{MAB}=\frac{1}{2}AB.MH=\frac{1}{2}.4,8.3,2=7,68\left(cm^2\right)\)

Do MA là tiếp tuyến \(\Rightarrow OA\perp MA\) hay tam giác OAM vuông tại A
Áp dụng định lý Pitago:
\(MA=\sqrt{OM^2-OA^2}=\sqrt{\left(\dfrac{8R}{5}\right)^2-R^2}=\dfrac{R\sqrt{39}}{5}\)
Theo t/c hai tiếp tuyến cắt nhau ta có \(AM=BM\)
Mà \(OA=OB=R\Rightarrow OM\) là trung trực AB \(\Leftrightarrow\left\{{}\begin{matrix}OM\perp AB\\AK=BK\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông OAM:
\(AK.OM=OA.AM\Rightarrow AK=\dfrac{OA.AM}{OM}=\dfrac{R\sqrt{39}}{8}\)
\(\Rightarrow AB=2AK=\dfrac{R\sqrt{39}}{4}\)
Áp dụng định lý Pitago trong tam giác vuông AOK:
\(OK=\sqrt{OA^2-AK^2}=\sqrt{R^2-\left(\dfrac{R\sqrt{39}}{8}\right)^2}=\dfrac{5R}{8}\)