Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M thuộc (d1) nên M(1-2t;1+t)
Theo đề, ta có: d(M;d2)=d(M;d3)
=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)
=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|
=>|-2t+3|=|-11t+3|
=>-2t+3=-11t+3 hoặc -2t+3=11t-3
=>t=0 hoặc t=6/13
=>M(1;1); M(1/13; 19/13)

Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D

Giao điểm A của d1 và d2 là nghiệm:
\(\left\{{}\begin{matrix}x+2y+1=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=11\\y=-6\end{matrix}\right.\)
\(\Delta\) song song d3 nên nhận (2;3) là 1 vtpt, nên có pt:
\(2\left(x-11\right)+3\left(y+6\right)=0\Leftrightarrow2x+3y-4=0\)

Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
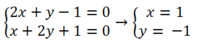
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.

Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)

a) Giao điểm d1 và d2
\(\left\{{}\begin{matrix}x+3y-1=0\\x-3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\) => A (-2;1)
Đường thẳng d3 có \(\overrightarrow{n_{d3}}=\left(2;-1\right)\) . Delta vuông góc với d3 nên có
\(\overrightarrow{u_{\Delta}}=\left(2;-1\right)\) \(\Rightarrow\overrightarrow{n_{\Delta}}=\left(-1;-2\right)\)
PTđt delta
\(-1\left(x+2\right)+\left(-2\right)\left(y-1\right)=0\)
\(\Leftrightarrow-x-2y+1=0\)
b) Tương tự, tìm được đường thẳng delta đi qua B(-1;-1)
Hệ số k = tan45 = 1 .
Tự xử nốt

Chọn B.
Gọi M(xM; yM) là giao điểm của d1 và d2. Khi đó, tọa độ giao điểm M của d1 và d2 là nghiệm của hệ phương trình:
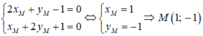
Để 3 đường thẳng d1, d2, d3 đồng quy thì M(1;-1) ∈ (d3): mx - y - 7 = 0, nên ta có:
m.1 - (-1) - 7 = 0 ⇔ m + 1 - 7 = 0 ⇔ m - 6 = 0 ⇔ m = 6
Vậy 3 đường thẳng d1, d2, d3 đồng quy.

Do các đường thẳng đôi một cắt nhau tại các điểm A, B, C nên các điểm cách đều các cạnh gồm tâm đường tròn nội tiếp và ba tâm đường tròn bàng tiếp.
Vậy có tất cả 4 điểm M cách đều ba đường thẳng đã cho.
đáp án D