Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B N M
Gọi NM là trung trực AB
=> NA = NB và góc MNA = góc MNB = 90o (Tính chất đường trung trực)
Xét tam giác MNA và tam giác MNB có:
góc MNA = góc MNB (= 90o)
Chung NM
NA = NB (cmt)
=> tam giác MNA = tam giác MNB (c.g.c)
=> MA = MB (2 cạnh tương ứng)


a) Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)
Cho đoạn thẳng AB, điểm M nằm trên đường trung trực của AB. So sánh độ dài các đoạn thẳng MA ,và MB.

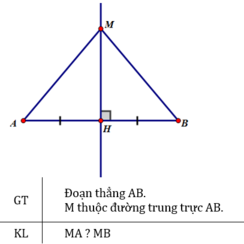
Gọi H là giao điểm của đường trung trực với đoạn AB
⇒ H là trung điểm AB và MH ⊥ AB.
Xét ΔAHM và ΔBHM có:

Nên ΔAHM = ΔBHM
Vậy MA = MB


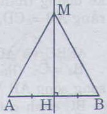
Gọi giao điểm của 2 đoạn thẳng AB và đg trung trực là H
HA=HB=3 cm
Xét tam giác vuông AHM , ta có
AM2= AH2+MH2 ( định lý py-ta-go)
hay AM2= 32+42= 9 +16= 25
=> AM=\(\sqrt{25}\)=5 cm
mà MA=MB (gt)
=> MA=MB=5cm
Chúc bạn học tốt

Hình vẽ: tự vẽ
Đặt AB vuông góc với đường trung trực tại E.
Xét 2 TG AME và BME, ta có:
AE=BE(gt); AEM=BEM=90o; ME; cạnh chung.
=>TG AME=TG BME(c.g.c)
=>MA=MB(2 cạnh tương ứng).
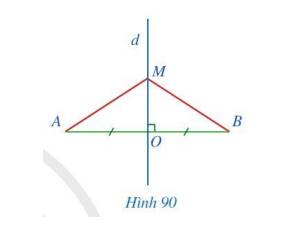
Cậu tự vẽ hình nhé (theo tớ) !! Cho CD là trung trực của AB, O là giao điểm, kẻ 1 điểm M bất kì. Nối A với M, B với M
Bài làm
Xét tam giác AOM và BOM
Có AO = OB (GT)
Góc O1 = O2 ( CD là trung trực của AB)
OM cạnh chung
=> Tam giác AOM = BOM (c.g.c)
=> MA = MB ( 2 cạnh tương ứng )
>> Nhớ cho mik nhé ! ❤