Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)

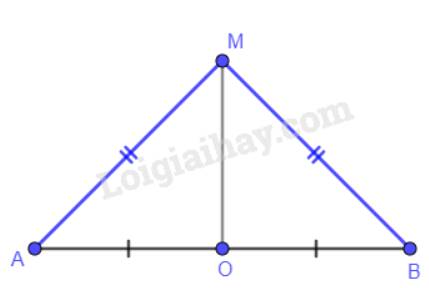
a) Xét hai tam giác MOA và MOB có:
OA = OB (O là trung điểm của AB);
MO chung;
MA = MB.
Vậy \(\Delta MOA = \Delta MOB\)(c.c.c).
b) \(\Delta MOA = \Delta MOB\)nên \(\widehat {MOA} = \widehat {MOB} = \dfrac{1}{2}\widehat {AOB} = 90^\circ \)hay \(MO \bot AB\).
Vậy MO có là đường trung trực của đoạn thẳng AB (MO đi qua trung điểm O của đoạn thẳng AB và vuông góc với đoạn thẳng AB).

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

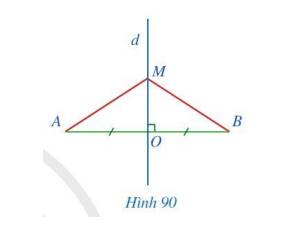
a: MC+CB=MB
mà CB=CA
nên MC+CA=MB
mà MC+CA<MA
nên MA>MB
b: Gọi D là giao điểm của NA với d
C là giao điểm của CB với d
Ta có:NA=ND+DA
mà DA=DB
nen NA=ND+DB(3)
mà NB<ND+DB
nên NA>NB

d H A B C 1 2 D
Giải:
Vì d là đường trung trực của AB và cắt AB tại H
\(\Rightarrow AH=HB\) (*)
Xét \(\Delta HAC,\Delta HBC\) có:
AH = HB ( theo (*) )
\(\widehat{AHC}=\widehat{BHC}\left(=90^o\right)\)
CH: cạnh chung
\(\Rightarrow\Delta HAC=\Delta HBC\left(c-g-c\right)\)
\(\Rightarrow CA=CB\) ( hai cạnh tương ứng ) ( đpcm )
b) Vì \(\Delta HAC=\Delta HBC\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\) ( góc tương ứng )
Xét \(\Delta CAD,\Delta CBD\) có:
\(CA=CB\)
\(\widehat{C_1}=\widehat{C_2}\)
CD: cạnh chung
\(\Rightarrow\Delta CAD=\Delta CBD\left(c-g-c\right)\)
Xin lỗi nhé, câu hỏi câu a là thế này:
Chứng minh tam giác HAC bằng tam giác HBC. Từ đó suy ra CA = CB ( H là giao điểm của d với AB)

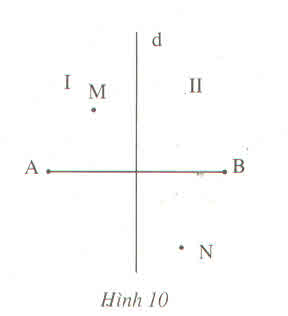
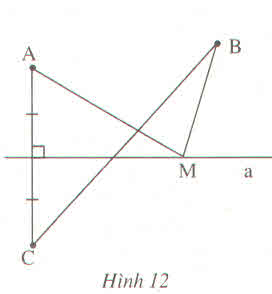
a: Gọi N là giao điểm của BC với a
Nếu M khác N
Vì M nằm trên đường trung trực của AC
nên MA=MC
XétΔMBC có BC<MB+MC
=>BC<MA+MB
Nếu M trùng với N thì nối NA
Vì N nằm trên đường trung trực của AC nên NA=NC
=>MA+MB=NA+NB=BC
=>MA+MB>=BC
b: MA+MB nhỏ nhất khi M là giao điểm của BC với a
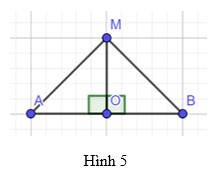

Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB
Xét tam giác AOM và tam giác BOM có :
OM là cạnh chung
AO = OB
\(\widehat {MOA} = \widehat {MOB} = {90^o}\)(do d là trung trực AB)
(c-g-c)
\( \Rightarrow MA = MB\) (cạnh tương ứng)