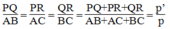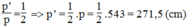Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

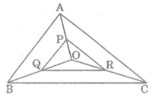
Xét tam giác PAC,ta có:
{MP=MAOP=OC{MP=MAOP=OC
=>MP = 1212 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 54325432 cm
LÀM LIỀU !!
Nối M với C ; B với P ; N với A
Xét tam giác OMC có : MP là đường trung tuyến ứng với cạnh OC
=> S MOP = S MCP = 1/2. S OMC ( t/c đường trung tuyến trong tam giác )
Xét tam giác AOC có : CM là đường trung tuyến ứng với cạnh OA
=> S OCM = S ACM = 1/2. S OAC ( t/c đường trung tuyến của tam giác )
=> S OMP = 1/4.S OAC
Tương tự CM được S ONP = 1/4 S OBC ; S OMN = 1/4. S OAB
=> S OMP + S OMN + S ONP = 1/4. S OAC + 1/4. S OAB + 1/4 . S OMN
=> S MNP = 1/4. S ABC
=> S MNP / S ABC = 1/4

Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm

Xét ΔOAB có
M,N lần lượt là trung điểm của OA,OB
=>MN là đường trung bình của ΔOAB
=>\(MN=\dfrac{1}{2}AB\)
Xét ΔOAC có
M,P lần lượt là trung điểm của OA,OC
=>MP là đường trung bình của ΔOAC
=>\(MP=\dfrac{1}{2}AC\)
Xét ΔOBC có
N,P lần lượt là trung điểm của OB,OC
=>NP là đường trung bình của ΔOBC
=>\(NP=\dfrac{1}{2}BC\)
Chu vi tam giác MNP là:
MN+NP+MP
\(=\dfrac{1}{2}\left(AB+CA+BC\right)\)
\(=\dfrac{1}{2}\cdot5,5=2,75\left(m\right)\)

Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm

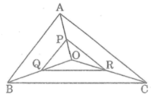
* Trong △ AOB ta có:
P trung điểm của OA (gt)
Q trung điếm của OB (gt)
Suy ra PQ là đường trung bình của △ AOB
Suy ra: PQ = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 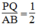 (1)
(1)
* Trong △ OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra PR là đường trung bình của tam giác OAC.
Suy ra: PR =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 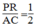 (2)
(2)
* Trong △ OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra QR là đường trung bình của tam giác OBC
Suy ra: QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 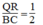 (3)
(3)
Từ (1), (2) và (3) suy ra: 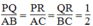
Vậy △ PQR đồng dạng △ ABC (c.c.c)

PM là đường trung bình của \(\Delta ABC\) nên \(PM=\frac{1}{2}AC\)
Mà PM cũng là ĐTB của \(\Delta OA'C'\) nên \(PM=\frac{1}{2}A'C'\)
Suy ra: \(AC=A'C'\)
Tương tự, ta có: \(PN=\frac{1}{2}BC,PN=\frac{1}{2}B'C'\Rightarrow BC=B'C'\)
\(MN=\frac{1}{2}AB,MN=\frac{1}{2}A'B'\Rightarrow AB=A'B'\)
Vậy \(\Delta ABC=\Delta A'B'C'\left(c.c.c\right)\)
Chúc bạn học tốt.