Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-2=-x+1\\y=-x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
a)
 b, Gọi giao điểm của 2 đường thẳng trên là M(x1;y1)
b, Gọi giao điểm của 2 đường thẳng trên là M(x1;y1)
tọa độ giao điểm của (d1) và (d2) là nghiệm của hpt
{y1=2x1−7y1=−x1−1{y1=2x1−7y1=−x1−1<=>{x1=2y1=−3{x1=2y1=−3
Vậy...
c, phương trình đường thẳng (d3) có dạng y=ax+b
Vì đt(d3) song song với (d2) và cắt đường thẳng (d1) tại một điểm nằm trên trục tung nên ta được a=-1, x=0,y=-7
=> b=-7
Thay a=-1, b=-7 vào cths y=ax+b ta được
y=-x-7

a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C

a: 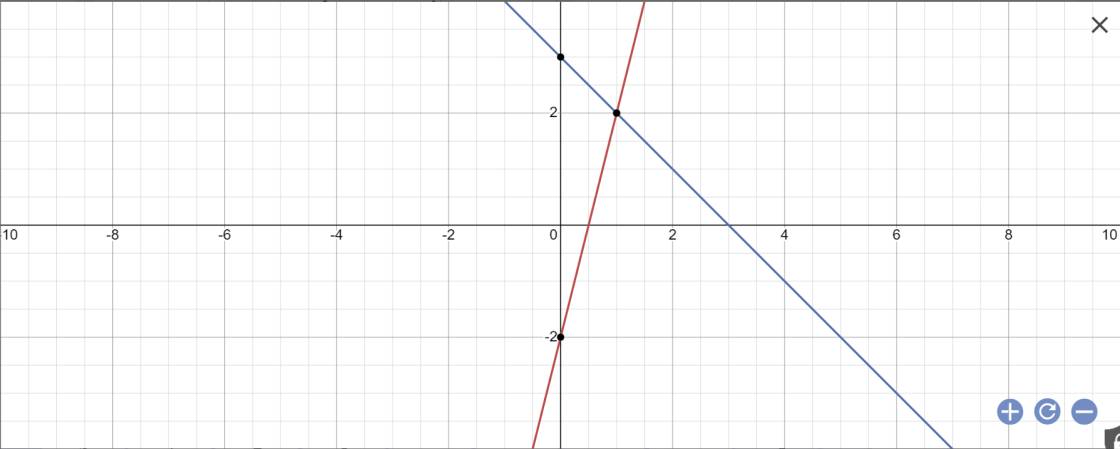
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)

1: Để hai đường thẳng cắt nhau thì
2m+1<>m+2
hay m<>1

a: 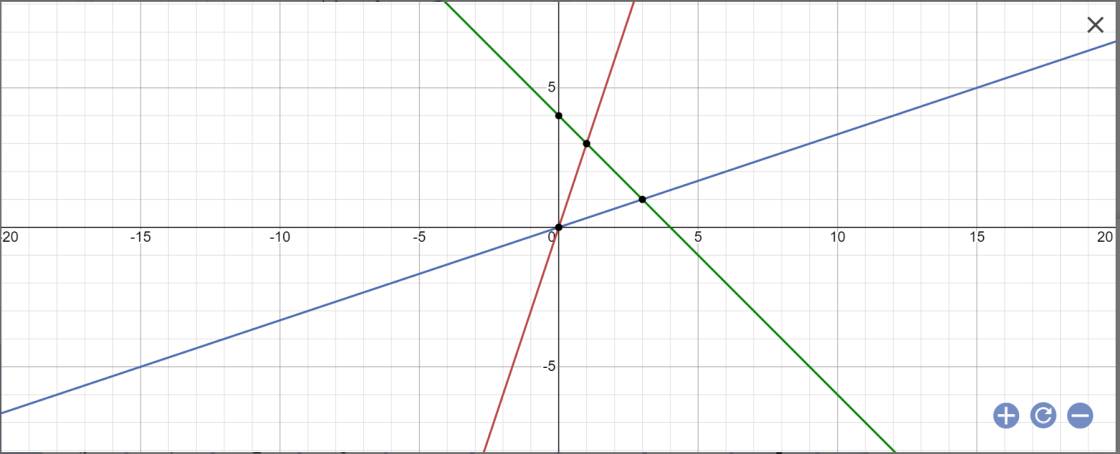
b:
Bổ sung đề: A,B lần lượt là giao của (d1) với (d2) và (d3)
Tọa độ A là:
3x=1/3x và y=3x
=>x=0 và y=0
Tọa độ B là:
3x=-x+4 và y=3x
=>x=1 và y=3
Ta có phương trình hoàng độ giao điểm:
4x−3=−x+2
⇔5x=5
⇔x=1
⇒y=−x+2=−1+2=1
Vậy 2 đồ thị cắt nhau tại A(1;1)
1 2 3 1 2 3 -1 -2 -3 y=4x-3 y=-x+2 A
Ta có phương trình hoàng độ giao điểm:
\(4x-3=-x+2\)
\(\Leftrightarrow5x=5\)
\(\Leftrightarrow x=1\)
\(\Rightarrow y=-x+2=-1+2=1\)
Vậy 2 đồ thị cắt nhau tại \(A\left(1;1\right)\)