Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
FG=FD
G,F,D thẳng hàng
Do đó: F là trung điểm của GD
Xét tứ giác ADCG có
F là trung điểm chung của AC và GD
=>ADCG là hình bình hành
Hình bình hành ADCG có AC\(\perp\)GD
nên ADCG là hình thoi

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó; E là trung điểm của AB
Xét ΔBAC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
Xét tứ giác ADBM có
E là trung điểm chung của AB và DM
=>ADBM là hình bình hành
c: Xét tứ giác ADCN có
F là trung điểm chung của AC và DN
=>ADCN là hình bình hành
=>AN//CD và AN=CD
Ta có: ADBM là hình bình hành
=>AM//BD và AM=BD
Ta có: AN//CD
AM//BD
mà B,D,C thẳng hàng
nên AN//BC và AM//BC
mà AN,AM có điểm chung là A
nên N,A,M thẳng hàng
Ta có: AM=BD
AN=CD
mà BD=DC
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN

a: Xét tứ giác AFCD có
E là trung điểm chung của AC và FD
=>AFCD là hình bình hành
b: EG//AB
AB\(\perp\)AC
Do đó: EG\(\perp\)AC
c:
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)

a: Sửa đề; DA=EF
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nen AEDF là hình chữ nhật
=>DA=EF
b: Xét tứ giác AFEH có
AF//HE
AF=HE
Do đó: AFEH là hình bình hành
XétΔABC có
Dlà trung điểm của BC
DE//AC
Do đó E là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DF//AB
Do đó:F là trung điểm của AC
Xét tứ giác AHBD có
E là trung điểm chung của AB và HD
AB vuông góc với HD
Do đó: AHBD là hình thoi
=>AB là phân giác của góc HAD(1)
c: Xét tứ giác ADCI có
F là trung điểm chung của AC và DI
DA=DC
Do đó: ADCI là hình thoi
=>AC là phân giác của góc DAI(2)
Từ (1), (2) suy ra góc IAH=2*90=180 độ
=>I,A,H thẳng hàng
mà AI=AH
nên A là trung điểm của IH
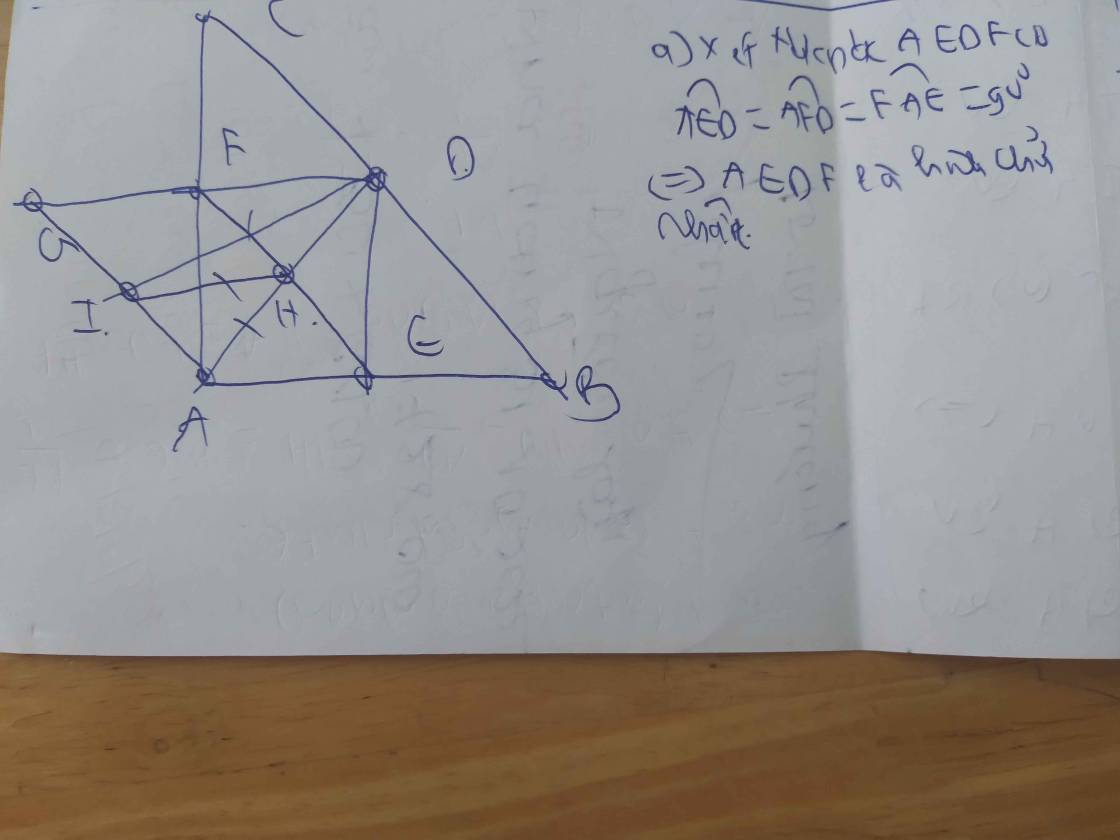



a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔADM có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
ΔADM cân tại A
mà AE là đường cao
nên AE là phân giác của \(\widehat{DAM}\left(1\right)\)
Xét ΔADN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔADN cân tại A
=>AD=AN
ΔADN cân tại A
mà AF là đường cao
nên AF là phân giác của \(\widehat{DAN}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAN}=\widehat{MAD}+\widehat{NAD}\)
\(=2\left(\widehat{EAD}+\widehat{FAD}\right)\)
\(=2\cdot\widehat{FAE}=2\cdot90^0=180^0\)
=>M,A,N thẳng hàng(3)
AM=AD
AN=AD
Do đó: AM=AN(4)
Từ (3) và (4) suy ra A là trung điểm của MN
c: Xét ΔADB và ΔAMB có
AD=AM
\(\widehat{DAB}=\widehat{MAB}\)
AB chung
Do đó: ΔADB=ΔAMB
=>\(\widehat{AMB}=\widehat{ADB}=90^0\)
=>BM\(\perp\)MN(5)
Xét ΔADC và ΔANC có
AD=AN
\(\widehat{DAC}=\widehat{NAC}\)
AC chung
Do đó: ΔADC=ΔANC
=>\(\widehat{ANC}=\widehat{ADC}=90^0\)
=>CN\(\perp\)NM(6)
Từ (5) và (6) suy ra BM//CN
Xét tứ giác BMNC có
BM//CN
BM\(\perp\)MN
Do đó: BMNC là hình thang vuông