Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

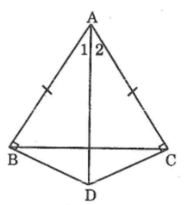
Xét hai tam giác vuông ABD và ACD, ta có:
∠(ABD) =∠(ACD) =90o
Cạnh huyền AD chung
AB = AC (giả thiết)
⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)
Suy ra: ∠(A1 ) =∠(A2) (hai góc tương ứng)
Suy ra AD là tia phân giác góc A

A B C _ _ D
Ta có:
ABD=ABC+CBD
ACD=ACB+BCD
Mà ABD=ACD (=90o)
ABC=ACB (\(\Delta\)ABC cân)
\(\Rightarrow\)CBD=BCD
\(\Rightarrow\Delta\)BDC cân
Xét \(\Delta\)ABD và \(\Delta\) ACD có:
AB=AC (\(\Delta\)ABC cân)
AD: chung
BD=CD (\(\Delta\)BDC cân)
\(\Rightarrow\Delta\)ABD=\(\Delta\)ACD (c.c.c)
\(\Rightarrow\)BAD=CAD (2 góc tương ứng)
\(\Rightarrow\)AD là p/g BAC (đpcm)
Ta có tam giác ABC la tam giác cân tại A
=> AB = AC ( tính chất tam giác cân )
Xét tam giác ABD vuông tại B và tam giác ACD vuông tại C có :
AB = Ac ( cmt )
Ad là cah chung
=> tam giác ABD = tam giác ACD ( ch -cgv )
=> Góc A1 = góc A2 ( hai góc tương ứng )
=> AD là tia phân giác góc A

Xét tam giác ADB và tam giac ADC có :
AD chung
Góc ABD=góc ACD=90 0
AB=AC(2 tam giác cân tại a)
=>tam giác ADB=tam giác ADC (ch-cgv)
=>góc BAD = góc CAD (góc tương ứng)
Vậy AD là tia phân giác góc A
Duyệt nha
Xét tam giác ADB và tam giác ADC có:
AD chung
góc ABD=góc ACD=90 độ
AB=AC(tam giác ABC cân tại A)
=> tam giác ADB=tam giác ADC(ch-cgv)
=> góc BAD=góc CAD(góc tương ứng)
Vậy AD là tia phân giác góc A
tik cho mk nha các bn
