
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


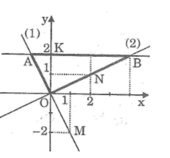
Qua điểm C trên trục tung có tung độ bằng 2, kẻ đường thẳng song song với Ox cắt đồ thị hàm số y = x tại D, cắt đồ thị hàm số y = 0,5x tại E.
Điểm D có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = x ta được x = 2.
Vậy điểm D(2; 2)
Điểm E có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = 0,5x ta được x = 4
Vậy điểm E(4; 2)
Gọi D’ và E’ lần lượt là hình chiếu của D và E trên Ox.
Ta có: OD’ = 2, OE’ = 4
Áp dụng định lí Pi-ta-go vào tam giác vuông ODD’, ta có:
O D 2 = O D ' 2 + D D ' 2 = 2 2 + 2 = 8
Suy ra: OD = 8 = 2 2
Áp dụng định lí Pi-ta-go vào tam giác vuông OEE’, ta có:
20 O E = O E ' 2 + E E ' 2 = 4 2 + 2 2 = 20
Suy ra: OE = 20 = 2 5
Lại có: DE = CE – CD = 4 – 2 = 2
Chu vi tam giác ODE bằng: OD + DE + EO = 2 2 + 2 + 2 5
= 2 2 + 1 + 5
Diện tích tam giác ODE bằng: 1/2.DE.OC = 1/2.2.2 = 2

a: tọa độ giao điểm M là:
\(\left\{{}\begin{matrix}2x-1=-x+2\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)

a: Đặt (d1): y=ax+b(a<>0)
Vì (d1) vuông góc với (d) nên 3a=-1
=>\(a=-\dfrac{1}{3}\)
Vậy: (d1): \(y=-\dfrac{1}{3}x+b\)
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x=-b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{x}{3}=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3b\\y=0\end{matrix}\right.\)
=>A(3b;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{3}\cdot0+b=b\end{matrix}\right.\)
=>B(0;b)
\(AB=2\sqrt{10}\)
=>\(AB^2=40\)
=>\(\left(0-3b\right)^2+\left(b-0\right)^2=40\)
=>\(10b^2=40\)
=>\(b^2=4\)
=>b=2 hoặc b=-2
Vậy: (d1): y=-1/3x+2 hoặc (d1): y=-1/3x-2
b: Đặt (d2): y=ax+b
Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-5\end{matrix}\right.\)
Vậy: (d2): y=3x+b
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\3x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{b}{3}\end{matrix}\right.\)
=>\(C\left(-\dfrac{b}{3};0\right)\)
tọa độ D là:
\(\left\{{}\begin{matrix}x=0\\y=3x+b=3\cdot0+b=b\end{matrix}\right.\)
=>D(0;b)
\(OC=\sqrt{\left(-\dfrac{b}{3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{b}{3}\right)^2+0}=\dfrac{\left|b\right|}{3}\)
\(OD=\sqrt{\left(0-0\right)^2+\left(b-0\right)^2}=\sqrt{0^2+b^2}=\left|b\right|\)
Vì Ox\(\perp\)Oy nên OC\(\perp\)OD
=>ΔOCD vuông tại O
=>\(S_{OCD}=\dfrac{1}{2}\cdot OC\cdot OD\)
=>\(S_{OCD}=\dfrac{\dfrac{1}{2}\left|b\right|}{3}\cdot\left|b\right|=\dfrac{1}{2}\cdot\dfrac{b^2}{3}\)
Để \(S_{OCD}=6\) thì \(\dfrac{b^2}{6}=6\)
=>\(b^2=36\)
=>\(b=\pm6\)
Vậy: (d2): y=3x+6 hoặc (d2): y=3x-6
Để ΔOCD cân tại O thì OC=OD
=>\(\dfrac{\left|b\right|}{3}=\left|b\right|\)
=>\(\left|b\right|=0\)
=>b=0
Vậy: (d2): y=3x