Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

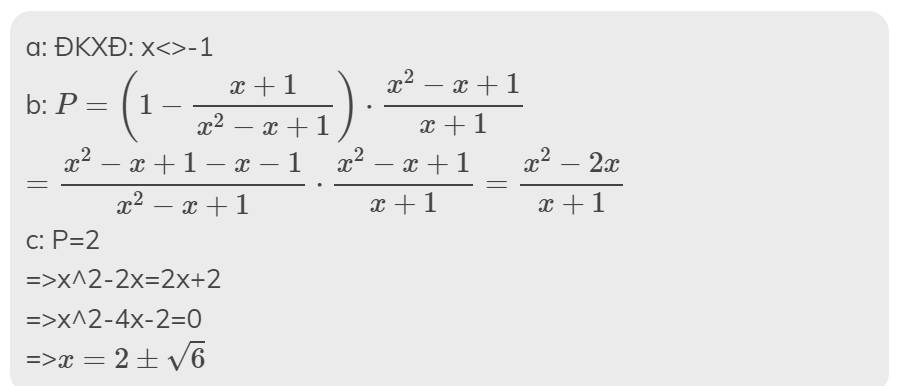
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)

a) Phân thức B xác định \(\Leftrightarrow\hept{\begin{cases}2x-2\ne0\\x^2-1\ne0\\2x+2\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne1\\x\ne\left\{\pm1\right\}\\x\ne-1\end{cases}\Leftrightarrow}x\ne\left\{\pm1\right\}}\)
b) \(B=\left(\frac{x+1}{2x-2}+\frac{3}{x^2-1}-\frac{x+3}{2x+2}\right)\cdot\frac{4x^2-4}{5}\)
\(B=\left[\frac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}+\frac{3\cdot2}{2\left(x-1\right)\left(x+1\right)}-\frac{\left(x+3\right)\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\frac{\left(2x\right)^2-2^2}{5}\)
\(B=\frac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\cdot\frac{\left(2x-2\right)\left(2x+2\right)}{5}\)
\(B=\frac{10\cdot2\left(x-1\right)\cdot2\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)\cdot5}\)
\(B=\frac{40\left(x-1\right)\left(x+1\right)}{10\left(x-1\right)\left(x+1\right)}\)
\(B=4\)
Vậy với mọi giá trị của x thì B luôn bằng 4
Vậy giá trị của B không phụ thuộc vào biến ( đpcm )
\(Giải:\)
\(ĐKXĐ:x\ne\pm1\)
\(B=\left[\frac{x+1}{2x-2}+\frac{3}{x^2-1}-\frac{x+3}{2x+2}\right]=\left[\frac{x+1}{2x-2}+\frac{12}{4x^2-4}-\frac{x+3}{2x+2}\right]\)
\(=\left[\frac{x+1}{2x-2}+\frac{12}{\left(2x+2\right)\left(2x-2\right)}-\frac{x+3}{2x+2}\right]\)
\(=\left[\frac{\left(x+1\right)\left(2x+2\right)}{\left(2x+2\right)\left(2x-2\right)}+\frac{12}{\left(2x+2\right)\left(2x-2\right)}-\frac{\left(x+3\right)\left(2x-2\right)}{\left(2x-2\right)\left(2x+2\right)}\right]\)
\(=\frac{2x^2+4x+14-2x^2+2x-6x+6}{\left(2x-2\right)\left(2x+2\right)}\)
\(=\frac{6}{\left(2x-2\right)\left(2x+2\right)}\)

Câu a :
ĐKXĐ : \(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(A=\left(\dfrac{x^2-2x}{2x^2+8x}-\dfrac{2x^2}{8-4x+2x^2-x^3}\right)\left(1-\dfrac{1}{x}-\dfrac{2}{x^2}\right)\)
\(=\left(\dfrac{\left(x^2-2x\right)\left(x-2\right)+2.2x^2}{2\left(x-2\right)\left(x^2+4\right)}\right)\left(\dfrac{x^2-x-2}{x^2}\right)\)
\(=\dfrac{x}{2\left(x-2\right)}\times\dfrac{\left(x+1\right)\left(x-2\right)}{x^2}\)
\(=\dfrac{x+1}{2x}\)
Câu b : Dễ rồi