Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ĐKXĐ: \(x\ne0;x\ne6;x\ne-6\)
b) \(A=\left(\dfrac{x}{x^2-36}-\dfrac{x-6}{x^2+6x}\right):\dfrac{2x-6}{x^2+6x}+\dfrac{x}{6-x}\)
\(A=\left[\dfrac{x}{\left(x+6\right)\left(x-6\right)}-\dfrac{x-6}{x\left(x+6\right)}\right]:\dfrac{2\left(x-3\right)}{x\left(x+6\right)}+\dfrac{x}{6-x}\)
\(A=\left[\dfrac{x^2}{x\left(x+6\right)\left(x-6\right)}-\dfrac{\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right]:\dfrac{2\left(x-3\right)}{x\left(x+6\right)}+\dfrac{x}{6-x}\)
\(A=\dfrac{x^2-x^2+12x-36}{x\left(x+6\right)\left(x-6\right)}:\dfrac{2\left(x-3\right)}{x\left(x+6\right)}+\dfrac{x}{6-x}\)
\(A=\dfrac{12x-36}{x\left(x+6\right)\left(x-6\right)}:\dfrac{2\left(x-3\right)}{x\left(x+6\right)}+\dfrac{x}{6-x}\)
\(A=\dfrac{12\left(x-3\right)}{x\left(x+6\right)\left(x-6\right)}:\dfrac{2\left(x-3\right)}{x\left(x+6\right)}-\dfrac{x}{x-6}\)
\(A=\dfrac{12\left(x-3\right)}{x\left(x+6\right)\left(x-6\right)}\cdot\dfrac{x\left(x+6\right)}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(A=\dfrac{6}{x-6}-\dfrac{x}{x-6}\)
\(A=\dfrac{6-x}{x-6}\)
\(A=-\dfrac{x-6}{x-6}\)
\(A=-1\)
Vậy giá trị của A không phụ thuộc vào giá trị của biến

Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
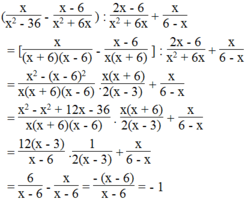
Vậy biểu thức không phụ thuộc vào biến x.

a) Phân thức xác định khi: \(\Leftrightarrow x-3\ne3\Leftrightarrow x\ne3\)
ĐKXĐ: \(x\ne3\)
b) \(A=\frac{2x^2+6x}{x^2-9}=\frac{2x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{2x}{x-3}\)
c) Thay x = -4 vào phân thức đã thu gọn, ta có:
\(A=\frac{2.\left(-4\right)}{\left(-4\right)-3}=\frac{8}{7}\)
Vậy: tại x = -4 là \(\frac{8}{7}\)
a) \(x^2-9=\left(x-3\right)\left(x+3\right)\)
Phân thức xác định khi: \(\left(x-3\right)\left(x+3\right)\ne0\)
\(\Leftrightarrow\hept{\begin{cases}x-3=0\\x+3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\x=-3\end{cases}}\Leftrightarrow x\ne\pm3\)
ĐKXĐ: \(x\ne\pm3\)
b) \(A=\frac{2x^2+6x}{x^2-9}=\frac{2x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{2x}{x-3}\)
c) \(A=\frac{2.\left(-4\right)}{\left(-4\right)-3}=\frac{8}{7}\)

\(A=6x^2+3x+2x+1-\left(6x^2-x+6x-1\right)\)
=\(6x^2+5x+1-6x^2-5x+1\)
\(=2\)
Suy ra biểu thức có giá trị không phụ thuộc vào biến.
\(B=2x^3+x^2+x-2x^2-x-1-\left(2x^3+3x^2+6x-4x^2-6x-12\right)\)
\(=2x^3-x^2-1-2x^3+x^2+12\)
\(=11\)
Suy ra biểu thức có giá trị không phụ thuộc vào biến.
a,
A=(2x+1)(3x+1)-(6x-1)(x+1)
=6x2+2x+3x+1-(6x2+6x-x-1
=6x2+2x+3x+1-6x2-6x+x+1
=6x2-6x2+2x+3x-6x+x+1+1
=2
Đpcm
b,
B=(x-1)(2x2+x+x)-(x-2)(2x2+3x+6)
=2x3+x2+x-2x2-x-1-(2x3+3x2+6x-4x2-6x-12)
=2x3+x2+x-2x2-x-1-2x3-3x2-6x+4x2+6x+12
=2x3-2x3+x2-2x2-3x2+4x2+x-x-6x+6x-1+12
=11
Đpcm

A = (2x - 3)(3x + 5) - (x - 1)(6x + 2) + 3 - 5x
= 6x2 + 10x - 9x - 15 - 6x2 - 2x + 6x + 2 + 3 - 5x
= (6x2 - 6x2) + (10x - 9x - 2x + 6x - 5x) - (15 - 2 - 3)
= -10
Vậy A ko phụ thuộc vào giá trị của biến x
a, A = 6x^2+x-15-6x^2+4x+2+3-5x = -10
=> Gía trị của biểu thức A ko phụ thuộc vào giá trị của biến
k mk nha