Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ: x>=0; x<>1
b \(A=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
c: Khi x=9-4 căn 5 thì \(A=\dfrac{1}{\sqrt{5}-2+2}=\dfrac{\sqrt{5}}{5}\)
d: căn x+2>=2
=>A<=1/2
Dấu = xảy ra khi x=0

a: ĐKXĐ: x>=0; x<>1
\(P=\dfrac{-3+\sqrt{x}-1}{x-1}\cdot\dfrac{\sqrt{x}+1}{1}=\dfrac{\sqrt{x}-4}{\sqrt{x}-1}\)
b: Để P=5/4 thì \(\dfrac{\sqrt{x}-4}{\sqrt{x}-1}=\dfrac{5}{4}\)
=>\(5\sqrt{x}-5=4\sqrt{x}-16\)
=>căn x=-11(loại)

1) a) Căn thức có nghĩa \(\Leftrightarrow4-2x\ge0\Leftrightarrow2x\le4\Leftrightarrow x\le2\)
b) Thay x = 2 vào biểu thức A, ta được: \(A=\sqrt{4-2.2}=\sqrt{0}=0\)
Thay x = 0 vào biểu thức A, ta được: \(A=\sqrt{4-2.0}=\sqrt{4}=2\)
Thay x = 1 vào biểu thức A, ta được: \(A=\sqrt{4-2.1}=\sqrt{2}\)
Thay x = -6 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-6\right)}=\sqrt{16}=4\)
Thay x = -10 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-10\right)}=\sqrt{24}=2\sqrt{6}\)
c) \(A=0\Leftrightarrow\sqrt{4-2x}=0\Leftrightarrow4-2x=0\Leftrightarrow x=2\)
\(A=5\Leftrightarrow\sqrt{4-2x}=5\Leftrightarrow4-2x=25\Leftrightarrow x=\frac{-21}{2}\)
\(A=10\Leftrightarrow\sqrt{4-2x}=10\Leftrightarrow4-2x=100\Leftrightarrow x=-48\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Thay x=9 vào A, ta được:
\(A=\dfrac{3-1}{3+1}=\dfrac{1}{2}\)
c: Ta có: P=AB
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\left(\dfrac{\sqrt{x}+3}{\sqrt{x}+1}+\dfrac{4}{\sqrt{x}-1}+\dfrac{5-x}{x-1}\right)\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\left(\dfrac{x+2\sqrt{x}-3+4\sqrt{x}+4+5-x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\cdot\dfrac{6\sqrt{x}+6}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{6}{\sqrt{x}+1}\)

\(a,ĐK:x>0;x\ne9\\ b,A=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ A=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ c,A>\dfrac{2}{5}\Leftrightarrow\dfrac{2}{\sqrt{x}+3}-\dfrac{2}{5}>0\\ \Leftrightarrow\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{5}>0\\ \Leftrightarrow\dfrac{2-\sqrt{x}}{5\left(\sqrt{x}+3\right)}>0\\ \Leftrightarrow2-\sqrt{x}>0\left(\sqrt{x}+3>0\right)\\ \Leftrightarrow\sqrt{x}< 2\Leftrightarrow0< x< 4\)

Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
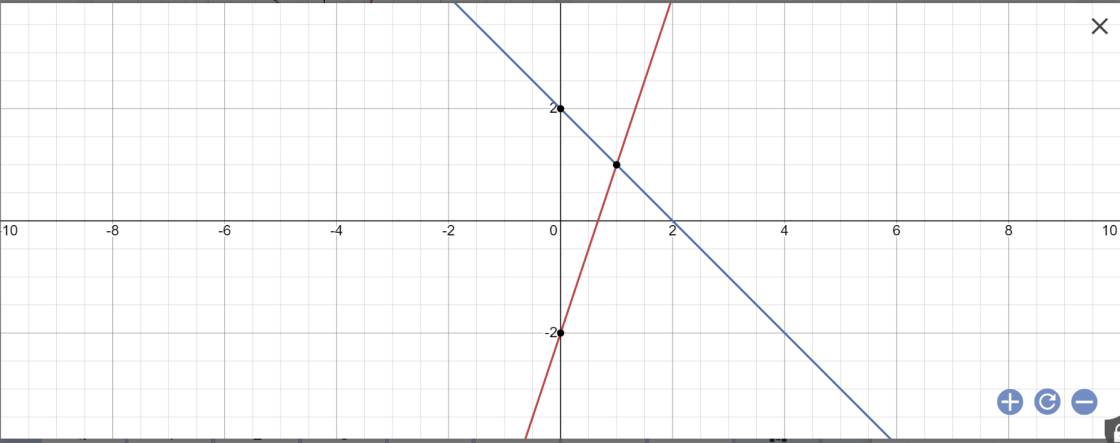
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)
a: ĐKXĐ: x>=0; x<>1
\(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{x+\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
b: Khi x=9/4 thì A=3/2:1/2=3/2*2=3