Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Cường độ trung bình là:
\(I\left(t\right)=\dfrac{Q\left(t\right)-Q\left(t0\right)}{t-t0}\)
b: Cho biết cường độ trung bình khi t chạy tới t0 thì ngày càng được thể hiện chính xác hơn, rõ ràng hơn.

Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s

Mấy câu trả lời SGK trình bày giúp anh Latex cái hoặc gõ ra nhưng gõ định dạng ấy em. Chứ như thế này anh sợ nhiều người không đọc được chữ ấy, mặc dù anh cũng đọc được.
Ta có:
\(\begin{array}{l}P'\left( t \right) = \frac{{{{\left( {500t} \right)}^\prime }\left( {{t^2} + 9} \right) - \left( {500t} \right){{\left( {{t^2} + 9} \right)}^\prime }}}{{{{\left( {{t^2} + 9} \right)}^2}}}\\ = \frac{{500\left( {{t^2} + 9} \right) - \left( {500t} \right).2t}}{{{{\left( {{t^2} + 9} \right)}^2}}}\\ = \frac{{500{t^2} + 4500 - 1000{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}} = \frac{{4500 - 500{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}}\end{array}\)
Tốc độ tăng dân số tại thời điểm \(t = 12\) là: \(P'\left( {12} \right) = \frac{{4500 - 500{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}} \approx - 2,88\).

Phương trình gia tốc là: \(a\left(t\right)=v'\left(t\right)=2t+2\)
a, Tại thời điểm t = 3(s), gia tốc tức thời là: \(a\left(3\right)=2\cdot3+2=8\left(m/s^2\right)\)
b, Vận tốc của chất điểm bằng 8
\(\Rightarrow t^2+2t-8=0\\ \Leftrightarrow\left(t-2\right)\left(t+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=2\\t=-4\left(loại\right)\end{matrix}\right.\)
Vậy khi t = 8s thì chất điểm đạt vận tốc 8m/s.

Ta có: \(s\in\left[-1;1\right]\Leftrightarrow-1\le2cos\left(\pi t\right)\le1\\ \Leftrightarrow-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\)
Trong 1s đầu tiên \(0< t< 1\Rightarrow0< \pi t< \pi\)
Ta có đồ thị hàm số \(y=cos\left(x\right)\) trên \(\left[0;\pi\right]\)
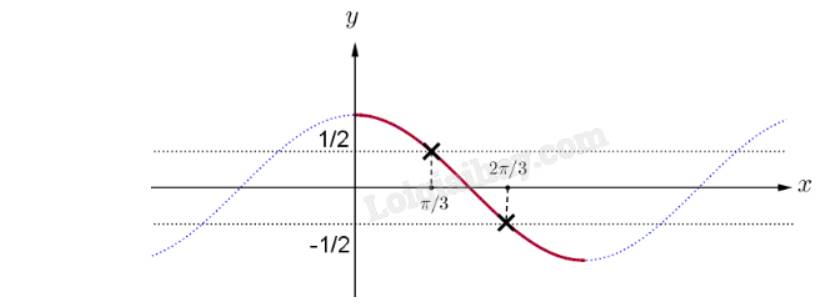
Dựa vào đồ thị, ta thấy
\(-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\Leftrightarrow\dfrac{\pi}{3}\le\pi t\le\dfrac{2\pi}{3}\Leftrightarrow\dfrac{1}{3}\le t\le\dfrac{2}{3}\)
Vậy \(t\in\left[\dfrac{1}{3};\dfrac{2}{3}\right]\)

Ta có s = 1 2 g t 2 => s ' ( t ) = g . t = v ( t )
Khi đó v ( 5 ) = 9 , 8.5 = 49 m/s
Chọn đáp án A

Hàm số \(T\left( t \right)\) có tập xác định là \(\left[ {0;100} \right]\).
Ta có: \(T\left( {60} \right) = 10 + 2.60 = 130\)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k - 3t} \right) = k - 3.60 = k - 180\\\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}\)
Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm \({t_0} = 60\)
Khi đó: \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k - 180 = 130 \Leftrightarrow k = 310\)
Vậy với \(k = 310\) thì hàm số \(T\left( t \right)\) liên tục trên tập xác định.

\(a,v\left(t\right)=s'\left(t\right)=3t^2-12t-9\)
Vận tốc của vật tại thời điểm t = 2s là: \(v\left(2\right)=3\cdot2^2-12\cdot2+9=-3\left(m/s\right)\)
Vận tốc của vật tại thời điểm t = 4s là: \(v\left(4\right)=3\cdot4^2-12\cdot4+9=9\left(m/s\right)\)
b, Khi vật đứng yên, ta có:
\(v\left(t\right)=0\Leftrightarrow3t^2-12t+9=0\Leftrightarrow\left[{}\begin{matrix}t=3\\t=1\end{matrix}\right.\)
c, Ta có \(a\left(t\right)=s"\left(t\right)=6t-12\)
Gia tốc của vật tại thời điểm t = 4s là \(a\left(4\right)=6\cdot4-12=12\left(m/s^2\right)\)
d, Ta có: Khi t = 1s hoặc t = 3s thì vật đứng yên.
Như vậy, ta cần tính riêng quãng đường vật đi được từng khoảng thời gian \(\left[0;1\right],\left[1;3\right],\left[3;5\right]\)
Từ thời điểm t = 0s đến thời điểm t = 1s, vật đi được quãng đường là:
\(\left|f\left(1\right)-f\left(0\right)\right|=\left|4-0\right|=4m\)
Từ thời điểm t = 1s đến thời điểm t = 3s, vật đi được quãng đường là:
\(\left|f\left(3\right)-f\left(1\right)\right|=\left|0-4\right|=4m\)
Từ thời điểm t = 3s đến thời điểm t = 5s, vật đi được quãng đường là:
\(\left|f\left(5\right)-f\left(3\right)\right|=\left|20-0\right|=20m\)
Tổng quãng đường vật đi được trong 5s đầu tiên là: 28m
e,Xét \(a\left(t\right)=0\Leftrightarrow t=2\)
Với \(t\in[0;2)\) thì gia tốc âm, tức là vật giảm tốc.
Với \(t\in(2;5]\) thì gia tốc dương, tức là vật tăng tốc.

Ta có:
\(T'\left(t\right)=-0,1\cdot2t+1,2=-0,2t+1,2\)
Tốc độ thay đổi của nhiệt độ ở thời điểm t = 1,5s là:
\(T'\left(1,5\right)=-0,2\cdot1,5+1,2=0,9\)

Dùng định nghĩa ta tính được Q'(t) = 4t + 1, từ đó suy ra cường độ dòng điện tại thời điểm t = 4(s) là I(4) = Q'(4) = 4.4 + 1 = 17
Chọn D