Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

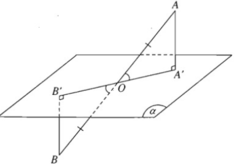
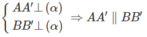
Mặt phẳng (AA', BB') xác định bởi hai đường thẳng song song (AA', BB') cắt mặt phẳng (α) theo giao tuyến qua O, A', B'. Do đó ba điểm O, A', B' thẳng hàng.
Hai tam giác vuông OAA'và OBB' bằng nhau vì có một cạnh huyền và một góc nhọn bằng nhau nên từ đó ta suy ra AA' = BB'.

Tham khảo:
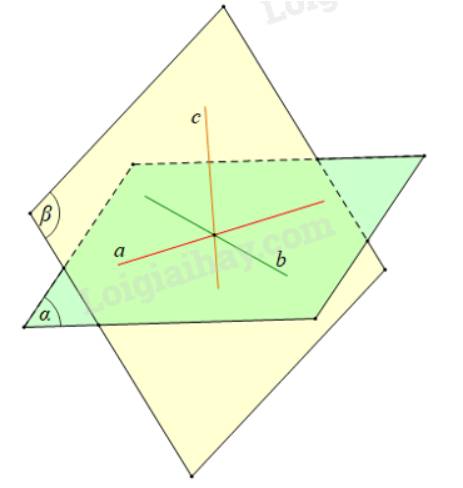
Giả sử a ∩ b = {I} và α = mp(a, b);
a ∩ c = {J} và β = mp(a, c);
b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.
Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.
α ∩ γ = b và đường thẳng b chính là đường thẳng IK.
β ∩ γ = c và đường thẳng c chính là đường thẳng JK.
Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)
Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.
Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.

SA vuông góc (P)
SA vuông góc (ABC)
=>(P)//(ABC)
=>B'C'//BC

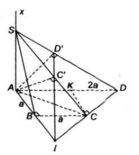
a) Ta có:
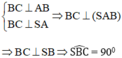
Gọi K là trung điểm của AD ta có CK = AB = AD/2 nên tam giác ACD vuông tại C
Ta có:
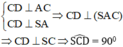
b) Trong mặt phẳng (SAC) vẽ AC’ ⊥ SC và trong mặt phẳng (SAD) vẽ AD’ ⊥ SD
Ta có AC’⊥ CD (vì CD ⊥ (SAC))
Và AC’ ⊥ SC nên suy ra AC’ ⊥ (SCD) ⇒ AC’ ⊥ SD
Ta lại có AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD) ⇒ AB ⊥ SD
Ba đường thẳng AD’, AC’ và AB cùng đi qua điểm A và vuông góc với SD nên cùng nằm trong mặt phẳng (α) qua A và vuông góc với SD
c) Ta có C’D’ là giao tuyến của (α) với mặt phẳng (SCD). Do đó khi S di động trên tia Ax thì C’D’ luôn luôn đi qua một điểm cố định là giao điểm của AB và CD
AB ⊂ (α), CD ⊂ (SCD) ⇒ I ∈ (α) ∩ (SCD) = C’D’

a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.

THAM KHẢO:
Vì AB và AC cùng vuông góc với một mặt phẳng (P) nên AB trùng AC
⇒⇒ A, B, C thẳng hàng.