Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)
góc A2 = xAC / 2
=> góc A2 = (góc ABC + C1) / 2 = B1 + ( C1 / 2 ) (Vì góc B1 = ABC /2 )
+) Trong tam giác AIB: góc AIB = 180o - (B1 + A1 + A2)
= 180o - (B1 + A1 +B1 + ( C1 / 2 ) )
= 180o - (2.B1 + A1 + ( C1 / 2 ) )
= 180o - (B + A1 + ( C1 / 2 ))
Mà B + A1 = 180o - C1 = 180o - 70o = 110o; C1 / 2 = 70o/ 2 = 35o
=> góc CIB = 180o - (110o + 35o) = 180o - 145o = 35o

Ta có:
ICK=ICB+KCB
=1/2ACB+1/2BCx
=1/2 180=90
Hoàn toàn tương tự thì:IBK=90
Xét tứ giác BICK có:
CIB+IBC+ICB+CKB=360
=>CIB=360-(IBC+ICB+CKB)=360-235=125
Vậy các góc của tứ giác BICK là CIB=125, CKB=55
IBK=ICK=90
hình bạn tự vẽ nha !chúc bạn học tốt

Bài 1 : Bài giải
Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)
Trong tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)
\(2\widehat{B}+150^o=360^o\)
\(2\widehat{B}=110^o\)
\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

Bài 1 :
Ta có :
B+BEF+BFE=180
D+DEF+DFE=180
mà B+D=180=>BEF+BFE+DEF+DFE=180
(BEF+BFE+DEF+DFE)/2=90
mà (BEF+DEF)/2=MEF;(BFE+DFE)/2=MFE
=>MEF+MFE=90=>EMF=90


a/Xét tứ giác ABCD có:
Góc C+D+DAB+CBA=360 độ
-> Góc C+D=3600-(DAB+CBA) (1)
Xét tam giác AEB có:
Góc AEB=1800-(EAB+EBA)
\(=180^o-\left(\frac{DBA}{2}+\frac{CBA}{2}\right)\)
\(=\frac{360-\left(DAB+CBA\right)}{2}\)
\(\Rightarrow AEB=360^o-\left(DAB+CBA\right)\) (2)
Từ (1) và (2) suy ra:
Góc AEB=D+C2D+C2
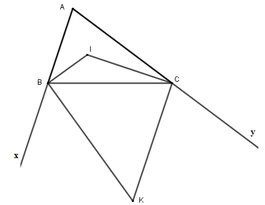
Kéo dài CA thành đường thẳng x, BD thành đường thẳng y.
Có: Góc CAB+BAx=1800
ABC+ABy=1800
-> Góc CAB=3600-(BAx+ABy) (3)
Xét tam giác AFB:
Góc AFB=1800-(FAB+FBA)
\(=180^o-\left(\frac{BAx+ABy}{2}\right)\)
\(\Rightarrow\frac{360-BAx+ABy}{2}\)
→2⋅AFB=3600−(Bax+ABy)→2⋅AFB=3600−(Bax+ABy) (4)
Từ (3) và (4) suy ra:
\(2.AFB=A+B\)
\(_{\Rightarrow AFB=\frac{A+B}{2}}\)