Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các số nguyên tố có một chữ số là : 2, 3, 5, 7
Điền vào dấu hỏi chấm ta được
Trong các phân số trên, các phân số viết được dưới dạng số thập phân hữu hạn là:
Vậy có thể điền ba số: 2, 3, 5
Để A viết được dưới dạng số thập phân hữu hạn thì y rút gọn với tử để mẫu chỉ chứa ước là 2 hoặc 5 hoặc y có ước là 2 hoặc 5
+ Nếu y rút gọn với mẫu để tử chứa ước là 2 hoặc 5
Do y nguyên tố nên y = 3
+ Nếu y có ước là 2 hoặc 5
Do y nguyên tố nên \(\left[\begin{array}{nghiempt}y=2\\y=5\end{array}\right.\)
Vậy có thể điền 3 số y nguyên tố thỏa mãn đề bài là 2; 3 và 5
hihi bài này mình học ùi nhưng ko hỉu cho a+2016 bạn về xem lại sách y
gọi số hs trung bình la a, hs giỏi là b, hs khá là c
theo bài ra ta có: a = 2c => \(\frac{a}{2}=\frac{c}{1}\) => \(\frac{a}{4}=\frac{c}{2}\) ( 1)
b = \(\frac{c}{2}\) (2)
từ 1 và 2 => \(\frac{a}{4}=\frac{c}{2}=\frac{b}{1}\) và a+b+c = 42
áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{4}=\frac{c}{2}=\frac{b}{1}=\frac{a+c+b}{4+2+1}=\frac{42}{7}=6\)
=> a= 24
b = 6
c = 12
vậy có 24 hs trung bình, 6 hs giỏi và 12 hs khá
Gọi số học sinh \(\text{giỏi; khá; trung bình}\) của lớp đó lần lượt là \(a;b;c\) \(\left(a;b;c\in N\text{*}\right)\) \(\left(\text{học sinh}\right)\)
Theo bài ra ta có : \(a+b+c=42\)
\(2b=c\Rightarrow b=\dfrac{c}{2}\) \(\left(1\right)\)
\(a=\dfrac{1}{2}b\Rightarrow a=\dfrac{b}{2}\Rightarrow2a=b\Rightarrow\dfrac{a}{\dfrac{1}{2}}=b\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra : \(\dfrac{a}{\dfrac{1}{2}}=b=\dfrac{c}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được :
\(\dfrac{a}{\dfrac{1}{2}}=b=\dfrac{c}{2}=\dfrac{a+b+c}{\dfrac{1}{2}+1+2}=\dfrac{42}{\dfrac{7}{2}}=12\)
\(\dfrac{a}{\dfrac{1}{2}}=12\Rightarrow a=6\\ \)
\(b=12\\ \)
\(\dfrac{c}{2}=12\Rightarrow c=24\)
\(\text{Vậy }a=6\\ b=12\\ c=24\)
cho bốn chữ số 2,3,4,1 a, viết tất cả các số khác nhau.b, tính tổng các số vừa viết một cách nhanh nhất
Minh viet khong dau ban chiu nha:
Goi so hoc sinh 3gioi, kha, trung binh lan luot la a;b;c(0<a;b;c<42)
theo bai ra,ta co:c=2b;a=1/2b
suy ra a:b:c=1:2:4 va a+b+c=42
Ap dung cong thuc day ti so bang nhau ta co:
a/1=b/2=c/4=a+b+c/1+2+4=42/7=6
Suy ra:a=6(hs)
b/2=6 suy ra b=2*6=12
c/4=6 suy ra c=6*4=24
Vay...
Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = , 5, 20 =
. 5, 125 =
đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn
Ta được;
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow\frac{a}{b}.\frac{c}{d}=\frac{a+c}{b+d}.\frac{a+c}{b+d}\)
\(\Rightarrow\frac{ac}{bd}=\frac{\left(a+c\right)^2}{\left(b+d\right)^2}\left(đpcm\right)\)
Giải:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk,c=dk\)
Ta có:
\(\frac{ac}{bd}=\frac{bkdk}{bd}=k^2\) (1)
\(\frac{\left(a+c\right)^2}{\left(b+d\right)^2}=\frac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\frac{\left[k.\left(b+d\right)\right]^2}{\left(b+d\right)^2}=\frac{k^2.\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\) (2)
Từ (1) và (2) suy ra \(\frac{ac}{bd}=\frac{\left(a+c\right)^2}{\left(b+d\right)^2}\left(đpcm\right)\)
Các số nguyên tố có một chữ số là : 2, 3, 5, 7
Điền vào dấu hỏi chấm ta được
Trong các phân số trên, các phân số viết được dưới dạng số thập phân hữu hạn là: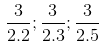
Vậy có thể điền ba số: 2, 3, 5