Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

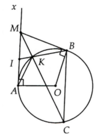
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)

1: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+DM=CD
nên CD=AC+BD
a: Xét (O) có
\(\widehat{IAK}\) là góc tạo bởi tiếp tuyến AI và dây cung AK
\(\widehat{IBA}\) là góc nội tiếp chắn cung AK
Do đó: \(\widehat{IAK}=\widehat{IBA}\)
Xét ΔIAK và ΔIBA có
\(\widehat{IAK}=\widehat{IBA}\)
\(\widehat{AIK}\) chung
Do đó: ΔIAK đồng dạng với ΔIBA