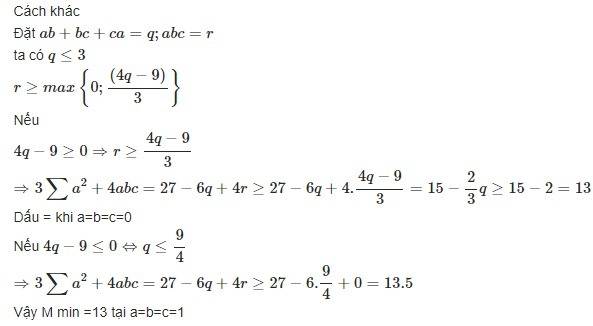PQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
0
LN
1
NY
27 tháng 12 2019
https://olm.vn/hoi-dap/detail/33622965541.html?pos=34266440529
Tham khảo này
PL
1
AH
Akai Haruma
Giáo viên
8 tháng 9 2024
Lời giải:
$A=a^3+b^3+ab=(a+b)^3-3ab(a+b)+ab=11^3-3ab.11+ab=1331-32ab$
$=1331-32a(11-a)=32a^2-352a+1331$
$=32(a^2-11a)+1331$
$=32(a^2-11a+5,5^2)+363=32(a-5,5)^2+363\geq 363$
Vậy $A_{\min}=363$
Giá trị này đạt tại $a-5,5=0\Leftrightarrow a=5,5$
TL
1
14 tháng 8 2017
a) Áp dụng bất đẳng thức Bnhiacopxki ta có :
\(\left(1^2+1^2+1^2\right)\left(a^2+b^2+c^2\right)\ge\left(a.1+b.1+c.1\right)^2\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=\frac{3^2}{3}=3\)
b) Ta có : \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)(đúng)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+ac+bc\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge3ab+3bc+3ac\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+ac+bc\right)\)
\(\Rightarrow ab+ac+bc\le\frac{\left(a+b+c\right)^2}{3}=\frac{3^2}{3}=3\)
9 tháng 3 2020
a) \(A=4x^2-12x+100=\left(2x\right)^2-12x+3^2+91=\left(2x-3\right)^2+91\)
Ta có: \(\left(2x-3\right)^2\ge0\forall x\inℤ\)
\(\Rightarrow\left(2x-3\right)^2+91\ge91\)
hay A \(\ge91\)
Dấu "=" xảy ra <=> \(\left(2x-3\right)^2=0\)
<=> 2x-3=0
<=> 2x=3
<=> \(x=\frac{3}{2}\)
Vậy Min A=91 đạt được khi \(x=\frac{3}{2}\)
b) \(B=-x^2-x+1=-\left(x^2+x-1\right)=-\left(x^2+x+\frac{1}{4}-\frac{5}{4}\right)=-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
Ta có: \(-\left(x+\frac{1}{2}\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\le\frac{5}{4}\) hay B\(\le\frac{5}{4}\)
Dấu "=" \(\Leftrightarrow-\left(x+\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow x+\frac{1}{2}=0\)
\(\Leftrightarrow x=\frac{-1}{2}\)
Vậy Max B=\(\frac{5}{4}\)đạt được khi \(x=\frac{-1}{2}\)
9 tháng 3 2020
\(C=2x^2+2xy+y^2-2x+2y+2\)
\(C=x^2+2x\left(y-1\right)+\left(y-1\right)^2+x^2+1\)
\(\Leftrightarrow C=\left(x+y-1\right)^2+x^2+1\)
Ta có:
\(\hept{\begin{cases}\left(x+y-1\right)^2\ge0\forall x;y\inℤ\\x^2\ge0\forall x\inℤ\end{cases}}\)
\(\Leftrightarrow\left(x+y-1\right)^2+x^2+1\ge1\)
hay C\(\ge\)1
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left(x+y-1\right)^2=0\\x^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=1\\x=0\end{cases}\Leftrightarrow}\hept{\begin{cases}y=1\\x=0\end{cases}}}\)
Vậy Min C=1 đạt được khi y=1 và x=0
7 tháng 4 2016
a, Ở phân số tử là a đầu tiên, thì nhân cả tử và mẫu cho c. Ở phân số thứ 2 có tử là b, nhân với ac, còn phân số còn lại giữ nguyên. Thì bạn sẽ có 3 phân số cùng mẫu nhé :3 Xong công vào ra 1 ^^
b, Viết bình phương (x+y+z)^2= bla blo :v Xong thay giữ kiện xy +yz+zx = 1 vào là done. Xong để có 10x^2+10y^2+z^2 thì dễ rồi nhé ^^
13 tháng 11 2019
a. Câu hỏi của Nguyễn Văn An - Toán lớp 8 - Học toán với OnlineMath
FT
3
YY
24 tháng 4 2017
\(P=a^3+b^3+c^3+a^2\left(b+c\right)+b^2\left(c+a\right)+c^2\left(a+b\right)\)
\(=a^3+a^2\left(b+c\right)+b^3+b^2\left(c+a\right)+c^3+c^2\left(b+a\right)\)
\(=a^2\left(a+b+c\right)+b^2\left(b+c+a\right)+c^2\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2\right)\)
\(=1\left(a^2+b^2+c^2\right)=a^2+b^2+c^2\)
T
10 tháng 2 2019
Tớ có cách khác:
Từ giả thiết suy ra:
\(P=a^3+b^3+c^3+a^2\left(1-a\right)+b^2\left(1-b\right)+c^2\left(1-c\right)\)\(=a^2+b^2+c^2\)
Lại có: \(a^2+\frac{1}{9}\ge2\sqrt{a^2.\frac{1}{9}}=\frac{2a}{3}\)
Suy ra \(a^2\ge\frac{2a}{3}-\frac{1}{9}\)
Thiết lập 2 BĐT còn lại tương tự và cộng theo vế:
\(P=a^2+b^2+c^2\ge\frac{2\left(a+b+c\right)}{3}-\frac{1}{9}=\frac{2}{3}-\frac{3}{9}=\frac{1}{3}\)
Dấu "=" xảy ra \(\Leftrightarrow a^2=b^2=c^2=\frac{1}{9}\Leftrightarrow a=b=c=\pm\frac{1}{3}\)
Vậy...