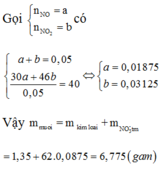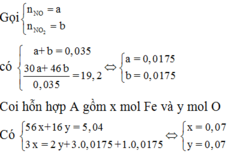Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo gt ta có: $n_{NO}=n_{NO_2}=0,0175(mol)$
Quy hỗn hợp A về Fe và O với số mol lần lượt là a;b(mol)
Ta có: $56a+16b=5,04(g);3a-2b=0,07(mol)$
Suy ra $a=b=0,07$
Vậy x=0,07
Coi A gồm Fe(x mol) ; O(y mol)
Suy ra: 56x + 16y = 5,04(1)
Gọi : \(\left\{{}\begin{matrix}n_{NO}=a\left(mol\right)\\n_{NO_2}=b\left(mol\right)\end{matrix}\right.\)
Suy ra: \(\left\{{}\begin{matrix}a+b=0,035\\30a+46b=0,035.2.19\end{matrix}\right.\)
Suy ra: a = 0,0175 ; b = 0,0175
\(Fe^0 \to Fe^{+3} + 3e\\ 2e+O^0 \to O^{-2} \\ 3e + N^{+5} \to N^+{+2}\\ 1e + N^{+5} \to N^{+4}\)
Bảo toàn e :
3x = 2y + 0,0175.3 + 0,0175.1(2)
(1)(2) suy ra: x = 0,07 ; y = 0,07
Vậy x = 0,07

Đáp án C
Gọi n N O = a n N O 2 = b
Có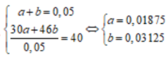
Vậy
m m u ố i = m k i m l o ạ i + m N O 3 -
=1 1,35+62.0,0875 = 6,775 (gam)

Ta có: \(n_{NO}+n_{NO_2}+n_{N_2}=\dfrac{22,4}{22,4}=1\left(mol\right)\left(1\right)\)
Mà: mX = 35,8 (g)
\(\Rightarrow30n_{NO}+46n_{NO_2}+28n_{N_2}=35,8\left(2\right)\)
Có: \(n_{Al}=\dfrac{32,4}{27}=1,2\left(mol\right)\)
\(n_{Cu}=\dfrac{22,4}{64}=0,35\left(mol\right)\)
BT e, có: 3nNO + nNO2 + 10nN2 = 3nAl + 2nCu = 4,3 (3)
Từ (1), (2) và (3) \(\Rightarrow\left\{{}\begin{matrix}n_{NO}=0,3\left(mol\right)\\n_{NO_2}=0,4\left(mol\right)\\n_{N_2}=0,3\left(mol\right)\end{matrix}\right.\)
⇒ nHNO3 = 4nNO + 2nNO2 + 12nN2 = 5,6 (mol)

\(n_k=0,6mol\)
\(d_k=d_{H_2}=26\Rightarrow d_k=52\)
Áp dụng sơ đồ đường chéo tính được là: \(n_{SO_2}=0,2mol;n_{NO_2}=0,4mol\)
Bảo toàn e: \(5^{+6}+2e\rightarrow S^{+4}\)
mol: \(0,4\rightarrow0,2\)
\(N^{+5}+1e\rightarrow N^{+4}\)
mol: \(0,4\rightarrow0,4\)
\(m_{\text{muối}}=m_{kl}+m_{SO_4^{2^-}}+m_{NO_3^-}=55,8g\)

a)\(\left\{{}\begin{matrix}n_{Cu}=x\left(mol\right)\\n_{Al}=y\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}64x+27y=9,1\\BTe:2x+3y=0,5\cdot1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0,1\\y=0,1\end{matrix}\right.\)
\(\%m_{Cu}=\dfrac{0,1\cdot64}{9,1}\cdot100\%=70,33\%\)
\(\%m_{Al}=100-70,33\%=29,67\%\)
b)\(\left\{{}\begin{matrix}n_{NO_2}+n_{NO}=0,5\\\dfrac{n_{NO_2}}{n_{NO}}=\dfrac{2}{1}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}n_{NO_2}=\dfrac{1}{3}\\n_{NO}=\dfrac{1}{6}\end{matrix}\right.\)
Gọi \(\left\{{}\begin{matrix}n_{Cu}=a\left(mol\right)\\n_{Al}=b\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}64a+27b=9,1\\BTe:2x+3y=\dfrac{1}{3}\cdot1+\dfrac{1}{6}\cdot3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{4}{115}\\b=\dfrac{527}{2070}\end{matrix}\right.\)
\(\%m_{Cu}=\dfrac{\dfrac{4}{115}\cdot64}{9,1}\cdot100\%=24,46\%\)
\(\%m_{Al}=100\%-24,46\%=75,54\%\)
\(n_{HNO_3}=2n_{NO_2}+4n_{NO}=2\cdot\dfrac{1}{3}+4\cdot\dfrac{1}{6}=\dfrac{4}{3}mol\)