Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho 4 điểm A, B, C, D cùng nằm trên đường thẳng d. Biết rằng điểm B nằm giữa hai điểm A và D, điểm C nằm giữa hai điểm B và D. Chứng tỏ rằng điểm B nằm giữa hai điểm A và C.
![]()
Vì C nằm giữa B và D è C và D nằm cùng phía với B (2)
Vì B nằm giữa A và D è A và D nằm khác phía với B (1)
Từ (1) và (2) è A và C nằm khác phía với B è B nằm giữa A và C.

nếu B nằm giữa A và D ,C nằm giữa A và D thì B nằm giữa A và C

Ta có : AC=5cm; BC=3cm và AD=7cm
=>CD=AD-AC=7-5=2cm
=>CD=2cm
=>AB=AC-BC=5-3=2cm
=>AB=2cm
=>AB=CD ( vì 2cm=2cm )
vì BC<AC(3<5)=>B nằm giữa A và C nên
AC=AB+BC
=>AB=AC-BC=5-3=2cm
vì AC<AD(5<7)=>C nằm giữa A và D nên
AD=AC+CD
=>CD=AD-AC=7-5=2cm
=>AB=CD(2=2)

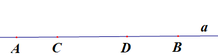
a/ Điểm B và D nằm cùng phía đối với điểm C;
Điểm A và D, A và B nằm khác phía đối với C
b/ CA và CD, CA và CB đối nhau; CB và CD trùng nhau
c/ Ta có: Điểm D nằm giữa B, C nên D ∈ CB (1)
Điểm C nằm giữa A, B nên hai tia CA, CB đối nhau (2)
Từ (1),(2) => CA, CD là hai tia đối nhau => C nằm giữa A, D.

![]()
Ta có C nằm giữa A, B nên CA, CB à hai tia đối nhau.
Mà D nằm giữa A và C nên D thuộc tia CA. Ta có CD,CB là hai tia đối nhau.
Do vậy C nằm giữa D và B.


Ta có C nằm giữa A, B nên CA, CB à hai tia đối nhau.
Mà D nằm giữa A và C nên D thuộc tia CA. Ta có CD,CB là hai tia đối nhau.
Do vậy C nằm giữa D và B.