Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

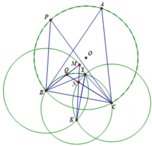
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.

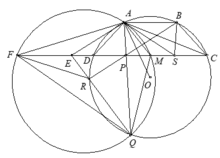
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.

a) Vì tam giác AFB đồng dạng với ACF(g.g) nên:
AF/AC=AB/AF hay AF^2=AB.AC => AF=căn(AB.AC) ko đổi 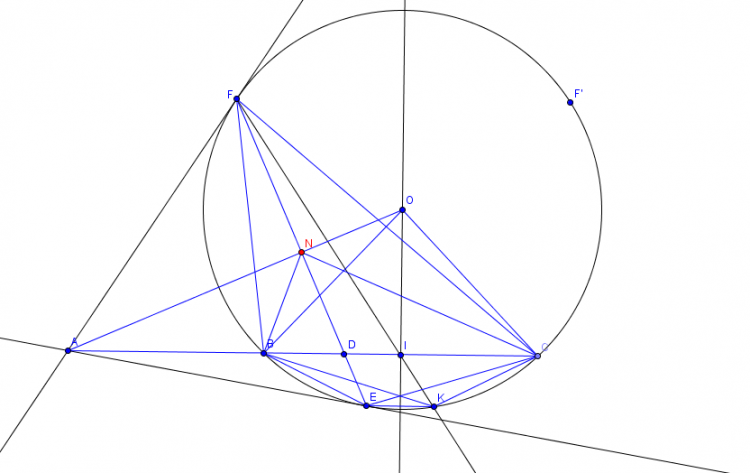
Mà AE=AF (T/cTtuyen) nên E, F cùng thuộc đường tròn bán kính căn(AB.AC)
b)Ta có: OI vuông góc với BC (T/ đường kính và dây)
Các điểm E, F, I cùng nhìn OA dưới 1 góc ko đổi 90 độ nên O,I,F,A,E cùng thuộc đường tròn đường kính OA
Ta có góc FIA=FOA(Cùng chắn cung FA trong đường tròn (OIFAE)
Mà góc FKE=FOA( Cùng bằng \(\frac{1}{2}\) góc FOE)
Suy ra góc FIA=FKE, nhưng hai góc này lại ở vị trí SLT nên KE//AB

\(C\left(M;R\right)\) đi qua \(F_2\Rightarrow MF_2=R\) (1)
\(C\left(M;R\right)\) tiếp xúc trong với \(C_1\left(F_1;2a\right)\Rightarrow MF_1=2a-R\) (2)
(1) + (2) cho \(MF_1+MF_2=2a\)
Vậy M di động trên elip (E) có hai tiêu điểm là \(F_1,F_2\) và trục lớn \(2a\)

A B C D E F O S K P G T L I M N
Bổ đề: Xét tam giác ABC có X và Y thuộc BC sao cho AX và AY đối xứng nhau qua phân giác góc BAC thì \(\frac{XB}{XC}.\frac{YB}{YC}=\frac{AB^2}{AC^2}\).
Giải bài toán:
Gọi đường thẳng đối xứng với PK qua phân giác của ^EPF cắt EF tại S. Ta sẽ chỉ ra S cố định, thật vậy:
Kéo dài KP cắt EF tại L, PE cắt KC tại T, PF cắt KB tại G, KP cắt GT tại I
Ta có ^GKT = ^PKB + ^PKC = ^PFB + ^PEC = ^PEF + ^PFE = 1800 - ^GPT, suy ra tứ giác PTKG nội tiếp
Suy ra ^PGT = ^PKT = ^PEC = ^PFE do đó GT // FE. Từ đó, áp dụng Bổ đề, ta có biến đổi tỉ số:
\(\frac{LE}{LF}.\frac{SE}{SF}=\frac{PE^2}{PF^2}\Leftrightarrow\frac{SE}{SF}=\frac{PE^2}{PF^2}.\frac{LF}{LE}=\frac{PT^2}{PG^2}.\frac{IG}{IT}=\frac{PT^2}{PG^2}.\frac{IG}{IP}.\frac{IP}{IT}=\frac{PT^2}{PG^2}.\frac{KG}{PT}.\frac{PG}{KT}\)
\(=\frac{PT}{PG}.\frac{KG}{KT}=\frac{ET}{FG}.\frac{KG}{KT}=\frac{KP}{BF}.\frac{CE}{KP}=\frac{CE}{BF}\)
Hạ BN,CM vuông góc với EF, ta dễ có \(\frac{SE}{SF}=\frac{CE}{BF}=\frac{CD}{BD}=\frac{EM}{FN}=\frac{SE+EM}{SF+FN}=\frac{SM}{SN}\)
Chú ý rằng BN // CM và cùng vuông góc EF, do vậy DS vuông góc EF. Mà D,E,F cố định nên S cố định
Vậy ta thu được điều phải chứng minh.

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
nên ABOC là tứ giác nội tiếp(1)
b: Xét tứ giác OEAC có
\(\widehat{OEA}+\widehat{OCA}=180^0\)
Do đó: OEAC là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,E,B,A,C cùng thuộc một đường tròn
c: \(\widehat{BIC}=\dfrac{sđ\stackrel\frown{BC}}{2}=\dfrac{\widehat{BOC}}{2}\)
mà \(\widehat{AOC}=\dfrac{\widehat{BOC}}{2}\)
nên \(\widehat{BIC}=\widehat{AOC}\)