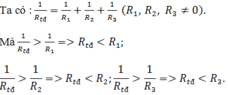Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
R1 R2 R3 A B + -
\(R_{12}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{6.12}{6+12}=4\left(\Omega\right)\)
\(R_{tđ}=\dfrac{R_{12}.R_3}{R_{12}+R_3}=\dfrac{4.18}{4+18}=\dfrac{36}{11}\left(\Omega\right)\)

a, R1 nt R2 // R3 // R4
=> \(\frac{1}{R_{234}}=\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}\) = \(\frac{1}{6}+\frac{1}{6}+\frac{1}{15}=\frac{2}{5}\) => R234 = 2,5 Ω
Rtđ = R1 + R234 = 5 + 2,5 = 7,5 Ω
b, Itđ = \(\frac{9}{7,5}=1,2\) A
Ta có Itđ = I1 = I234 = 1,2A
=> U1 = I1.R1 = 1,2.5 = 6 (V)
=> U234 = 9-6 = 3 (V)
Do R2//R3//R4 nên U2 = U3 = U4 = 3 V
=> I2 = I3 = 0,5 A
I4 = 0,2A

1, Câu A (vì để ko bị hỏng người ta chọn hiệu điện thế nhỏ nhất trong đoạn mạch)
2, Câu A (I toàn mạch sẽ bằng I1+I2=1A mà I=U/Rtđ => Rtđ= U/I=9/1=9Ω)
3,A ( Rtđ=(R1.R2)/R1+R2=8Ω =>I=U/Rtđ=3A;R1//R2 => U1=U2 mà R2=4R1 => I2=4I1 câu a hợp lý)
4,A ( Rtđ = U/I=24Ω. Ta có R1=2R2 ta lập phương trình: \(24=\frac{R2.2R2}{R2+2R2}=>R2=36;R1=2.36=72\)

a) Rtđ của đoạn mạch AB khi R1 mắc nối tiếp với R2 là: Rtđ = R1 + R2 = 20 + 20 = 40Ω.
Vậy Rtđ lớn hơn, mỗi điện trở thành phần.
b) Khi R1 mắc song song với R2 thì:
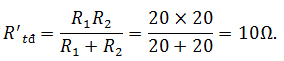
Vậy R'tđ nhỏ hơn mỗi điện trở thành phần.
c) Tỉ số giữa Rtđ và R'tđ là:
![]()

R1ntR2
\(=>R1+R2=100\Omega\)(1)
R1//R2
\(=>R_{td}=\dfrac{R1.R2}{R1+R2}=\dfrac{R1.R2}{100}=16\)
=>R1.R2=1600(2)
Từ (1)(2)
=> R1=20 \(\Omega\)
R2=80\(\Omega\)

Cấu tạo mạch : \(R_1nt\left(R_2\backslash\backslash R_3\right)\)
a/ \(R_{AB}=R_1+\frac{R_2.R_3}{R_2+R_3}=4+\frac{10.15}{10+15}=10\left(Ôm\right)\)
b/ \(I_A=\frac{U_{AB}}{R_{AB}}=\frac{5,4}{10}=0,54\left(A\right)=I_1=I_{23}\)
\(U_{23}=I_{23}.R_{23}=0,54.\frac{R_2.R_3}{R_2+R_3}=3,24\left(V\right)=U_2=U_3\)
\(I_2=\frac{U_2}{R_2}=\frac{3,24}{10}=0,324\left(A\right)\)
\(I_3=\frac{U_3}{R_3}=\frac{3,24}{15}=0,216\left(A\right)\)
Vậy...