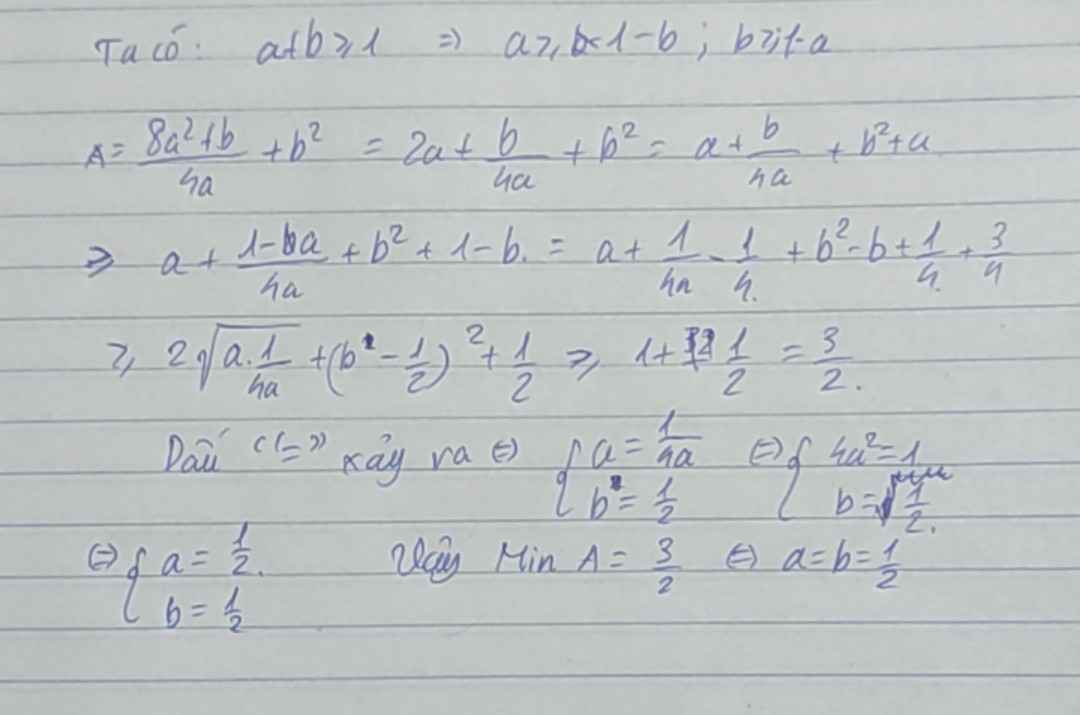Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{8a^2+b}{4a}+b^2=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(\ge a+1-b+\frac{1-a}{4a}+b^2=a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2\)(do \(a+b\ge1\))
\(=\left(a+\frac{1}{4a}\right)+b^2-b+\frac{1}{4}+\frac{1}{2}\)
\(\ge2\sqrt{a\cdot\frac{1}{4a}}+\left(b-\frac{1}{2}\right)^2+\frac{1}{2}\)
\(\ge2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\)
Dấu = khi \(a=b=\frac{1}{2}\)

Do \(0< a< 1\Rightarrow b>0\)
\(A=2a+\frac{b}{4a}+b^2=\frac{3a}{2}+\frac{a}{2}+\frac{b}{4a}+b^2\ge\frac{3a}{2}+3\sqrt[3]{\frac{ab^3}{8a}}=\frac{3}{2}\left(a+b\right)\ge\frac{3}{2}\)
\(A_{min}=\frac{3}{2}\) khi \(a=b=\frac{1}{2}\)

Lời giải:
Vì $a+b\geq 1\Rightarrow b\geq 1-a; a\geq 1-b$. Do đó:
\(A\geq \frac{8a^2+1-a}{4a}+b^2=2a+\frac{1}{4a}-\frac{1}{4}+b^2\)
\(\geq a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2=\left(a+\frac{1}{4a}\right)+(b^2-b+\frac{1}{4})+\frac{1}{2}\)
Áp dụng BĐT AM-GM: \(a+\frac{1}{4a}\geq 1\)
$b^2-b+\frac{1}{4}=(b-\frac{1}{2})^2\geq 0$
Do đó: $A\geq 1+0+\frac{1}{2}=\frac{3}{2}$
Vậy $A_{\min}=\frac{3}{2}$. Dấu "=" xảy ra khi $a=b=\frac{1}{2}$

\(A=2a+\frac{b}{4a}+b^2\)
Mà \(a+b\ge1\Leftrightarrow b\ge1-a\). Suy ra \(A\ge2a+\frac{1-a}{4a}+b^2=2a+\frac{1}{4a}-\frac{1}{4}+b^2=a+\frac{1}{4a}+a+b^2-\frac{1}{4}\)
Mà \(a+b\ge1\Leftrightarrow a\ge1-b\). Suy ra
\(A\ge a+\frac{1}{4a}+b^2-b+\frac{3}{4}=a+\frac{1}{4a}+b^2-b+\frac{1}{4}+\frac{1}{2}\)
Áp dụng bđt Cosi: \(\Rightarrow A\ge2+\left(b-\frac{1}{2}\right)^2+\frac{1}{2}\Leftrightarrow A\ge\frac{3}{2}\)
Dấu = xảy ra tại a=b=1/2