Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Xét tứ giác ACHI có: góc ACB = 90o (góc nội tiếp chắn nửa đường tròn)
góc HIA = 90o (gt)
=> tổng hai góc này =180o mà đỉnh C và I lại nằm ở vị trí đối nhau => tứ giác ACHI là tứ giác nội tiếp đường tròn đường kính AH (đpcm)

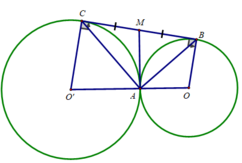
a) Ta có:
OB // O'C ( cùng vuông góc với d)
⇒ Tứ giác OBCO' là hình thang vuông
⇒ ∠(BOO') + ∠(CO'O) = 180 0
Δ CO'A cân tại O' có:
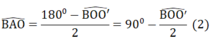
Từ (1) và (2):
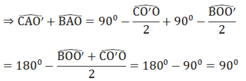
Lại có: ∠(CAO') + ∠(BAO) + ∠(BAC) = 180 0 ⇒ ∠(BAC) = 180 0 - 90 0 = 90 0
⇒ ΔABC vuông tại A.

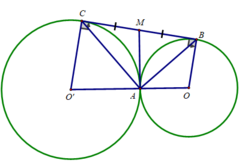
b) Ta có: M là trung điểm của cạnh huyền BC
⇒ MA = MB = MC
⇒ ΔMAB cân tại M ⇒ ∠(MAB ) = ∠(MBA )
Lại có: ΔOAB cân tại O ⇒ ∠(OAB ) = ∠(OBA )
⇒ ∠(MAB ) + ∠(OAB ) = ∠(MBA ) + ∠(OBA ) ⇔ ∠(MAO ) = ∠(MBO) = 90 0
⇒ MA là tiếp tuyến của (O)
Chứng minh tương tự: MA là tiếp tuyến của (O')
Vậy MA là tiếp tuyến chung của hai đường tròn (O) và (O')
Mn giải giúp mk vs
Help me pls ;-;