Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

n = 3 đúng.
Với n >=4. Từ 1 đỉnh của đa giác ta nối được với n - 2 đỉnh ( trừ 2 đỉnh liền kề ) ta được n-2 tam giác => dpcm.
Từ bài này ta đi đến cm được tổng các góc ngoài của 1 đa giác luôn bằng 360o.

a)Vẽ các đường chéo xuất phát từ một đỉnh của n - giác, ta được (n - 2) tam giác.
Tổng các góc của hình n - giác bằng tổng các góc của (n - 2) tam giác, tức là có số đo bằng (n - 2).1800.
b) ta có: (n - 2).1800 = (12 - 2 ).1800 = 18000

Gọi trung điểm của AD là P
trung điểm của BC là Q
=>PQ là đường trung bình của hình thang ABCD
=>MN//DC
Lại có góc ngoài của góc A và D kề nhau
=> hai tia phân giác của góc này hợp với nhau 1 góc 90 độ => góc M =90 độ
Tương tự có góc N =90 độ
Xét tam giác AMD có góc M =90 độ
P là trung điểm của AD
=> MP=PA=> tam giác MPA cân ở P => Góc MAP = góc AMP => MP//AB
Tương tự có QN//AB
mà MN//AB =>M, P, Q, N thẳng hàng
=>mn//\ba. Mà BA//DC => MN//DC
Bạn cho mình hỏi, ở đoạn suy ra PQ là đường trung bình của hình thang ABCD, rồi suy ra MN //DC là sao? Nếu đã suy ra được rồi thì cần gì phải chứng minh đoạn dưới nữa. Ở phần đó, bạn có viết nhầm hay không? Bạn giải thích giúp mình với

A B C N M E F G H I K
a) Kéo dài các tia AN; AE; AM; AF cho chúng cắt đường thẳng BC theo thứ tự tại các điểm G;H;I;K.
Xét \(\Delta\)ABI có: BM là phân giác ^ABI và BM vuông góc AI (tại M) => \(\Delta\)ABI cân tại B
=> BM đồng thời là đường trung tuyến \(\Delta\)ABI => M là trung điểm AI
C/m tương tự, ta có: N;E;F lần lượt là trung điểm của AG;AH;AK
Xét \(\Delta\)GAH: N là trung điểm AG; E là trung điểm AH => NE là đường trung bình \(\Delta\)GAH
=> NE // GH hay NE // BC (1)
Tương tự: MF // BC (2); NF // BC (3)
Từ (1); (2) và (3) => 4 điểm M;N;E;F thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).
b) Theo câu a ta có: NF là đường trung bình \(\Delta\)AGK => \(NF=\frac{GK}{2}=\frac{BG+BC+CK}{2}\)(*)
Lại có: \(\Delta\)ABG cân ở B; \(\Delta\)ACK cân ở C (câu a) nên BG = AB; CK = AC
Thế vào (*) thì được: \(NF=\frac{AB+BC+AC}{2}\),
KL: ...

a) - Vẽ các đường chéo xuất phát từ cùng 1 đỉnh của n - giác đã cho
=> n - giác gồm (n -2) tam giác từ mỗi 1 cạnh của n - giác và các đường chéo trên
Tổng 3 góc trong 1 tam giác bằng 180o => Tổng các góc trong của n - giác là: (n - 2).180o
+) Vì tại mỗi đỉnh của n - giác: Tổng góc trong và góc ngoài bằng 180o nên Tổng các góc trong và ngoài của hình n - giác (có n - đỉnh) bằng
n.180o
=> Tổng các góc ngoài của n - giác bằng: n.180o - (n - 2).180o = 360o
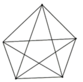
b) +) Mỗi đỉnh của n - giác nối với n - 1 đỉnh còn lại => được n -1 đường thẳng
Có n đỉnh => Vẽ được n(n - 1) đường thẳng
Trong đó, mỗi đường thẳng đều được tính 2 lần nên số đường thẳng vẽ được là: n(n -1)/2
n.(n - 1)/2 đường thẳng này có n cạnh của hình n - giác nên Số đường chéo có tất cả là: \(\frac{n\left(n-1\right)}{2}-n=\frac{n\left(n-3\right)}{2}\)
*) tính số đường chéo của tam giác => n = 3 => kết quả = 0

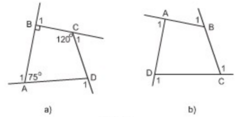
a) + Góc ngoài tại A là góc A1:
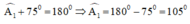
+ Góc ngoài tại B là góc B1:
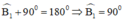
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
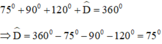
Lại có:
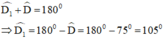
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
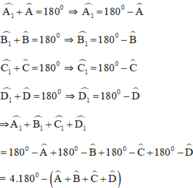
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
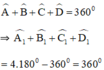
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.

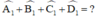
a) Vẽ các đường chéo từ đỉnh của n-giác , ta được ( n - 2 ) tam giác .
Tổng các góc của hình n-giác bằng tổng các góc của ( n - 2 ) tam giác và có số đo bằng ( n - 2 ) . 1800
Vậy tổng các góc ngoài của hình n-giác bằng ( n - 2 ) . 1800
b) Tổng số đo của góc trong và góc ngoài tại 1 đỉnh của hình n-giác bằng 1800 . Tổng số đo của góc trong và góc ngoài tại n đỉnh của hình n-giác bằng n.1800 . Tổng các góc của hình n-giác bằng ( n - 2 ) . 1800
Vậy tổng các góc ngoài của hình n-giác bằng : n . 1800 - ( n - 2 ) . 1800 = 3600 .
Nguyễn Thu Thủy làm đúng rồi nha khỏi làm lại )))