Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(A_t=\dfrac{hc}{\lambda_0}\Rightarrow \lambda_0=\dfrac{hc}{A_t}=\dfrac{6,625.10^{-34}.3.10^8}{4,5.1,6.10^{-19}}=0,276.10^{-6}m=0,276 \mu m\)
Hiện tượng quang điện xảy ra khi \(\lambda \le\lambda_0\)
Suy ra các bức xạ thỏa mãn là: \(\lambda_1,\lambda_2,\lambda_3\)

Đáp án C
Vận tốc ban đầu cực đại của các electron quang điện bằng:
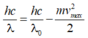
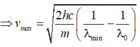
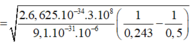
![]()

Ta có
Wđ= \(\frac{hc}{\lambda}\)
lấy tỉ lệ
1,5=\(\frac{hc}{1.2\lambda}\) => \(\lambda\)
sau đó A=\(\frac{hc}{\lambda}\)
không biết có đúng không. Nếu sai sót mong mn góp ý ạ![]()

a. Bước sóng của chùm sáng: \(\lambda=\dfrac{c}{f}=\dfrac{3.10^8}{10^{15}}=0,3\mu m\)
Giới hạn quang điện: \(\lambda_0=\dfrac{hc}{A_t}=\dfrac{6,625.10^{-34}.3.10^8}{5,15.1,6.10^{-19}}=0,24.19^-6m=0,24\mu m\)
Do \(\lambda > \lambda_0\) nên không xảy ra hiện tượng quang điện.
b. Ta có: \({W_{d0}} = \frac{{hc}}{\lambda } - A = 1,{7.10^{ - 19}}J\Rightarrow {v_0} = \sqrt {\frac{{2{W_{d0}}}}{m}} = 0,{6.10^6}m/s\)
c. \({n_e} = \frac{{{I_{bh}}}}{e} = 2,{8.10^{13}};\,\,\,\,\,\,{n_\lambda } = \frac{P}{{\frac{{hc}}{\lambda }}} = \frac{{P\lambda }}{{hc}} ={3.10^{15}} \Rightarrow H = \frac{{{n_e}}}{{{n_\lambda }}} = 9,{3.10^{ - 3}} = 0,93\% \)

Đáp án: C
Vận tốc ban đầu cực đại của các electron quang điện băng
h c λ = h c λ 0 + m v 1 2 2 ⇒ v 1 = 2 m . h c λ - h c λ 0 = 2 9 , 1 . 10 - 31 6 , 625 . 10 - 34 . 3 . 10 8 0 , 243 . 10 - 6 - 6 , 625 . 10 - 34 . 3 . 10 8 0 , 5 . 10 - 6

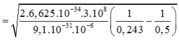
102 m/s