Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

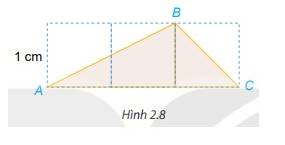
Ta có: \(AB \approx 2,2(cm);BC \approx 1,4(cm)\)
Vậy độ dài đường gấp khúc ABC là: \(AB + BC = 2,2 +1,4 = 3,6\) (cm)
Kết quả này trùng với kết quả ở bài tập 2.27

a) - Viết dạng thập phân vô hạn tuần hoàn:\(\dfrac{1}{9};\dfrac{1}{99}\) là: \(\dfrac{1}{9}=0,(1);\dfrac{1}{99}=0,(01)\)
- Nhận xét:
Dạng thập phân vô hạn tuần hoàn của phân số có dạng \(\dfrac{1}{99...9}\) như sau:
\(\dfrac{1}{99...9}= 0,(0…001) \) ( n chữ số 9); ( \(n-1\) chữ số 0)
b) Dự đoán kết quả của \(\dfrac{1}{999}\)
Theo nhận xét ở câu a ta có: \(\dfrac{1}{999}=0,(001)\)

ps đc viết dưới dạng số thập phân hữu hạn : \(\frac{1}{4};\frac{13}{50};-\frac{17}{125};\frac{7}{14}\)
ps đc viết dưới dạng só thập phân vô hạn tuần hoàn : \(-\frac{5}{6};\frac{11}{45}\)
\(\frac{1}{4}=0,25;\frac{13}{50}=0,26;-\frac{17}{125}=-0,136;\frac{7}{14}=0,5\)
\(-\frac{5}{6}=-0,8\left(3\right);\frac{11}{45}=0,2\left(4\right)\)

Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)

Giải thích: Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = 23, 5, 20 = 22.5, 125 = 53 đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn.
3/8 = 0,375 ; −7/5 = -1,4; 13/20 = 0,65 ; −13/125 = -0,104
b. Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 12=22.3, 22=2.11, 35=7.5, 65 = 5.13 đều có chứa thừa số nguyên tố khác 2 và 5 nên chúng được viết dưới dạng số thập phân vô hạn tuần hoàn
ta được : \(\frac{5}{12}=0.41\left(6\right);\frac{29}{22}=1.3\left(18\right);\frac{27}{35}=0.7;\frac{51}{65}=0.8\)

a)
\(\begin{array}{l}\frac{{17}}{3} = 5,(6);\\ - \frac{{125}}{111} = 1,(126);\\\sqrt 5 = 2,2360679....; \sqrt {19} = 4,3588989...\end{array}\)
b) Làm tròn số \( \sqrt {19} \) với độ chính xác 0,05, tức là làm tròn số 4,3588989… đến chữ số hàng phần mười, ta được 4,4.
a: \(\dfrac{17}{3}=5,\left(6\right);-\dfrac{125}{111}=-1,\left(126\right);\sqrt{5}\simeq2,24\)
\(\sqrt{19}\simeq4,36\)
b: \(\sqrt{19}\simeq4,4\)

Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)
a) Mỗi đoạn dây nhận được là: \(\frac{{10}}{7} = 1,(428571)\) (m)
b) Cách 1: Dùng thước đo, ta được mỗi đoạn dây dài 143 cm.
Chu vi hình vuông là: 4.143 = 572 cm
Cách 2: \(C = 4.\frac{{10}}{7}\) \( = 5,(714285) \approx 5,71\)(m)
Chú ý:
Với 2 cách đo đạc và tính toán, ta có thể nhận được kết quả chênh lệch (không đáng kể), tùy vào cách làm tròn.