Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khi a > 0, hàm số y = ax + b đồng biến trên khoảng (-∞; +∞) hay đồng biến trên R.
- Khi a < 0, hàm số y = ax + b nghịch biến trên khoảng (-∞; +∞) hay nghịch biến trên R.

Hàm số \(y=-f\left(x\right)\) đồng biến trên khoảng \(\left(a;b\right)\)

1.
a) Lấy $x_1\neq x_2\in (0;+\infty)$
Ta có:
\(\frac{y(x_1)-y(x_2)}{x_1-x_2}=\frac{\sqrt{x_1}-\sqrt{x_2}}{x_1-x_2}=\frac{1}{\sqrt{x_1}+\sqrt{x_2}}>0\)
\(\Rightarrow \) hàm số đồng biến trên $(0;+\infty)$
b) Lấy $x_1\neq x)2\in [1+\infty)$
Ta có:
\(\frac{y(x_1)-y(x_2)}{x_1-x_2}=\frac{\sqrt{x_1-1}-\sqrt{x_2-1}}{x_1-x_2}=\frac{1}{\sqrt{x_1-1}+\sqrt{x_2-1}}>0\)
Do đó hàm số đồng biến tập xác định $[1;+\infty)$
Lời giải:
a) Lấy $x_1,x_2\in\mathbb{R}; x_1\neq x_2$
Để $y=mx^3$ đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{m(x_1^3-x_2)^3}{x_1-x_2}>0$
$\Leftrightarrow m(x_1^2+x_1x_2+x_2^2)>0$
$\Leftrightarrow m>0$ (do $x_1^2+x_1x_2+x_2^2=(x_1+\frac{x_2}{2})^2+\frac{3}{4}x_2^2>0$ với mọi $x_1\neq x_2$
b)
Điều kiện: $m\leq 2$
Ta thấy, với $x_1\neq x_2\in (2;+\infty)$:
\(\frac{y(x_1)-y(x_2)}{x_1-x_2}=\frac{\sqrt{x_1-m}-\sqrt{x_2-m}}{x_1-x_2}=\frac{1}{\sqrt{x_1-m}+\sqrt{x_2-m}}>0\) với mọi $x\in (2;+\infty); m\leq 2$
Do đó hàm số đồng biến khi $m\leq 2$
c)
Lấy $x_1,x_2\in (0;+\infty)$. Để hàm số đồng biến trên $(0;+\infty)$ thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow (\frac{m}{x_1^2}-\frac{m}{x_2^2}).\frac{1}{x_1-x_2}>0$
$\Leftrightarrow \frac{-m(x_2+x_1)}{x_1^2x_2^2}>0$
$\Leftrightarrow -m>0$ (do $\frac{x_2+x_1}{x_1^2x_2^2}>0$ với mọi $x_1,x_2>0$
$\Leftrightarrow m< 0$

a) hệ số a=-2=>y luôn nghịch biến
b) a=1 >0 và -b/2a =-5 => (-5;+vc) y luôn đồng biến
c) hàm y có dạng y=a/(x+1)
a =-1 => y đồng biến (-vc;-1) nghich biến (-1;+vc
=>
(-3;-2) hàm y đồng biến
(2;3) hàm y đồng biến
a) Hàm số \(y=-2x+3\) có a = -2 < 0 nên hàm số nghịch biến trên R.
b. Xét tỉ số \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\left(x^2_1+10x_1+9\right)-\left(x^2_2+10x_2+9\right)}{x_1-x_2}\)
\(=\dfrac{\left(x_1-x_2\right)\left(x_1+x_2+10\right)}{x_1-x_2}=x_1+x_2+10\).
Với \(x_1;x_2\notin\left(-5;+\infty\right)\) thì \(x_1+x_2+10\ge0\) nên hàm số y đồng biến trên \(\left(-5;+\infty\right)\).
c) Xét tỉ số: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-\dfrac{1}{x_1+1}+\dfrac{1}{x_2+1}}{x_1-x_2}=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Trên \(\left(-3;-2\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}< 0\) nên hàm số y nghịch biến trên \(\left(-3;-2\right)\).
Trên \(\left(2;3\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}>0\) nên hàm số y đồng biến trên \(\left(2;3\right)\).

Xét hai số thực \(a;b\) bất kì thỏa mãn \(a>b>1\)
\(f\left(a\right)-f\left(b\right)=a+\frac{1}{a}-\left(b+\frac{1}{b}\right)=a-b+\frac{1}{a}-\frac{1}{b}\)
\(=a-b-\frac{a-b}{ab}=\left(a-b\right)\left(1-\frac{1}{ab}\right)\)
Do \(a>b>1\Rightarrow\left\{{}\begin{matrix}a-b>0\\ab>1\Rightarrow\frac{1}{ab}< 1\Rightarrow1-\frac{1}{ab}>0\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)-f\left(b\right)>0\Rightarrow f\left(a\right)>f\left(b\right)\)
Vậy hàm đồng biến trên \(\left(1;+\infty\right)\)
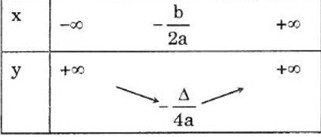

Nếu \(a>0\) thì hàm số \(y=ax^2+bx+c\)
Nghịch biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\);
Đồng biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\).
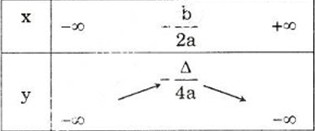
Nếu \(a< 0\) thì hàm số \(y=ax^2+bx+c\):
Nghịch biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\);
Đồng biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\).