Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.2^8.5^4}{5^{10}.2^{10}}=\dfrac{1}{5^2.2^2}=\dfrac{1}{25.4}=\dfrac{1}{100}\)
b, \(\dfrac{2^7.9^3}{6^5.8^2}=\dfrac{2^7.3^6}{2^5.3^5.2^6}=\dfrac{3}{2^4}=\dfrac{3}{16}\)
c, \(\dfrac{45^{10}.5^{20}}{75^5}=\dfrac{5^{10}.3^{20}.5^{20}}{3^5.5^{10}}=5^{20}.3^{15}\)
d, \(\left(0,8\right)^5=\left(0,1\right)^5.8^5=\dfrac{1}{100000}.32768=0,32768\)
e, \(\dfrac{2^{15}.9^4}{6^6.8^3}=\dfrac{2^{15}.3^8}{2^6.3^6.2^9}=3^2=9\)
d, \(\dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\dfrac{2^{40}.\left(2^{20}+1\right)}{2^{30}.\left(2^{20}+1\right)}=2^{10}=1024\)
Chúc bạn học tốt!!!
\(\text{a) }\dfrac{5^4\cdot20^4}{25^5\cdot4^5}=\dfrac{5^4\cdot\left(5\cdot4\right)^4}{\left(5^2\right)^5\cdot4^5}=\dfrac{5^4\cdot5^4\cdot4^4}{5^{10}\cdot4^5}=\dfrac{5^8\cdot4^4}{5^{10}\cdot4^5}=\dfrac{1}{5^2\cdot4}=\dfrac{1}{25\cdot4}=\dfrac{1}{100}\)
\(\text{b) }\dfrac{2^7\cdot9^3}{6^5\cdot8^2}=\dfrac{2^7\cdot\left(3^2\right)^3}{\left(2\cdot3\right)^5\cdot\left(2^3\right)^2}=\dfrac{2^7\cdot3^6}{2^5\cdot3^5\cdot2^6}=\dfrac{2^7\cdot3^6}{2^5\cdot2^6\cdot3^5}=\dfrac{2^7\cdot3^6}{2^{11}\cdot3^5}=\dfrac{3}{2^4}=\dfrac{3}{16}\)
\(\text{c) }\dfrac{45^{10}\cdot5^{20}}{75^5}=\dfrac{\left(5\cdot9\right)^{10}\cdot5^{20}}{\left(25\cdot3\right)^5}=\dfrac{5^{10}\cdot9^{10}\cdot5^{20}}{25^5\cdot3^5}=\dfrac{5^{10}\cdot5^{20}\cdot\left(3^2\right)^{10}}{\left(5^2\right)^5\cdot3^5}=\dfrac{5^{30}\cdot3^{20}}{5^{10}\cdot3^5}=5^{20}\cdot3^{15}\)
\(\text{d) }\left(0.8\right)^5=\left(\dfrac{8}{10}\right)^5=\left(\dfrac{4}{5}\right)^5=\dfrac{4^5}{5^5}=\dfrac{64}{3125}\)
\(\text{e) }\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}=\dfrac{2^{15}\cdot\left(3^2\right)^4}{\left(2\cdot3\right)^6\cdot\left(2^3\right)^3}=\dfrac{2^{15}\cdot3^8}{2^6\cdot3^6\cdot2^9}=\dfrac{2^{15}\cdot3^8}{2^6\cdot2^9\cdot3^6}=\dfrac{2^{15}\cdot3^8}{2^{15}\cdot3^6}=3^2=9\)
\(f\text{) }\dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\dfrac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}=1024\)

\(a,25^3:5^2=\left(5^2\right)^3:5^2=5^6:5^2=5^4\)
\(b,\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{9}{49}\right)^6=\)\(\left(\dfrac{3^{21}}{7^{21}}\right):\left(\dfrac{9^6}{49^6}\right)=\dfrac{3^{21}:7^{21}}{9^6:49^6}=\dfrac{3^{21}:7^{21}}{\left(3^2\right)^6:\left(7^2\right)^6}=\dfrac{3^{21}:7^{21}}{3^{12}:7^{12}}=3^9:7^9=\dfrac{3^9}{7^9}=\left(\dfrac{3}{7}\right)^9\)
\(c,\dfrac{4^2.43}{210}=\dfrac{\left(2^2\right)^2.43}{7.3.2.5}=\dfrac{2^4.43}{7.3.2.5}=\dfrac{2^3.43}{7.3.5}=\dfrac{344}{105}\)
\(d,\dfrac{2^7.9^3}{6^5.8^2}=\dfrac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\dfrac{2^7.3^6}{2^5.3^5.2^6}\) =\(\dfrac{2^7.3^6}{2^{11}.3^5}=\dfrac{3}{2^4}=\dfrac{3}{16}\)

a) \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2=\left(\dfrac{13}{14}\right)^2=\dfrac{169}{196}\)
b) \(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2=\left(\dfrac{-1}{12}\right)^2=\dfrac{1}{144}\)
c) \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{\left(5.20\right)^4}{\left(25.4\right)^5}=\dfrac{100^4}{100^5}=\dfrac{1}{100}\)
d) \(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4=\dfrac{-10^5}{3^5}.\dfrac{-6^4}{5^4}=\dfrac{-\left(2.5\right)^5.\left(3.2\right)^4}{3^5.5^4}=\dfrac{-29.5}{3}=-853\dfrac{1}{3}\)

a,
\(\dfrac{4^2\cdot4^3}{2^{10}}=\dfrac{4^5}{2^{10}}=\dfrac{\left(2^2\right)^5}{2^{10}}=\dfrac{2^{10}}{2^{10}}=1\)
b,
\(\dfrac{\left(0,6\right)^5}{\left(0,2\right)^6}=\dfrac{\left(0,2\cdot3\right)^5}{\left(0,2\right)^5\cdot0,2}=\dfrac{\left(0,2\right)^5\cdot3^5}{\left(0,2\right)^5\cdot0,2}=\dfrac{243}{0,2}=\dfrac{243}{\dfrac{1}{5}}=243\cdot5=1215\)
c,
\(\dfrac{2^7\cdot9^3}{6^5\cdot8^2}=\dfrac{2^7\cdot\left(3^2\right)^3}{\left(2\cdot3\right)^5\cdot\left(2^3\right)^2}=\dfrac{2^6\cdot2\cdot3^6}{2^5\cdot3^5\cdot2^6}=\dfrac{3}{2^4}=\dfrac{3}{16}\)
d,
\(\dfrac{6^3+3\cdot6^2+3^3}{-13}=\dfrac{\left(2\cdot3\right)^3+3\cdot\left(2\cdot3\right)^2+3^3}{-13}=\dfrac{2^3\cdot3^3+3\cdot2^2\cdot3^2+3^3}{-13}=\dfrac{2^3\cdot3^3+2^2\cdot3^3+3^3}{-13}\dfrac{3^3\left(2^3+2^2+1\right)}{-13}=\dfrac{3^3\cdot13}{-13}=-3^3=-27\)

a) \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2=\left(\dfrac{6}{14}+\dfrac{7}{17}\right)^2=\left(\dfrac{13}{12}\right)^2=\dfrac{13^2}{12^2}=\dfrac{169}{144}\)
b)\(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2=\left(\dfrac{9}{12}-\dfrac{10}{12}\right)^2=\left(\dfrac{-1}{12}\right)^2=\dfrac{\left(-1\right)^2}{12^2}=\dfrac{1}{144}\)
c)\(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.5^4.2^8}{5^{10}.2^{10}}=\dfrac{5^8.2^8}{5^8.5^2.2^8.2^2}=\dfrac{1}{5^2.2^2}=\dfrac{1}{25.4}=\dfrac{1}{100}\)
d)\(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4=\dfrac{\left(-10\right)^5.\left(-6\right)^4}{3^5.5^4}=\dfrac{\left(-2\right)^5.5^5.2^4.3^4}{3^4.3.5^4}=\dfrac{\left(-2\right)^5.5.5^42^4}{3.5^4}=\dfrac{\left(-2\right)^5.5.2^4}{3}=\dfrac{-2560}{3}=-853\dfrac{1}{3}\)

a.ta có :4^2.4^3/2^10=2^4.2^6/2^10=2^10/2^10=1
b. ta co :(0,6)^5/(0,2)^5=(0,6/0,2)^5=3^5=243

a, \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2=\left(\dfrac{3}{7}\right)^2+2.\dfrac{3}{7}.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\)
\(=\dfrac{9}{49}+\dfrac{3}{7}+\dfrac{1}{4}=\dfrac{169}{196}\)
b, \(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2=\left(\dfrac{3}{4}\right)^2-2.\dfrac{3}{4}.\dfrac{5}{6}+\left(\dfrac{5}{6}\right)^2\)
\(=\dfrac{9}{16}-\dfrac{5}{4}+\dfrac{25}{36}=\dfrac{1}{144}\)
c, \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.5^4.4^4}{5^{10}.4^5}=\dfrac{1}{5^2.4}=\dfrac{1}{100}\)
d, \(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4=\dfrac{\left(-10\right)^5}{3^5}.\dfrac{6^4}{5^4}\)
\(=\dfrac{5^5.\left(-2\right)^5.2^4.3^4}{3^5.5^4}=\dfrac{-\left(5.2^9\right)}{3}=\dfrac{-2560}{3}\)
Chúc bạn học tốt!!!

a) \(\dfrac{4^2.4^3}{(2^2)^5}=\dfrac{4^2.4^3}{4^5}=\dfrac{4^3}{4^3}=1\)
b) = 1215
c) = \(\dfrac{3}{16}\)
d) = (-27)

a.
\(\frac{2^7\times9^3}{6^5\times8^2}=\frac{2^7\times\left(3^2\right)^3}{\left(2\times3\right)^5\times\left(2^3\right)^2}=\frac{2^7\times3^6}{2^5\times3^5\times2^6}=\frac{3}{2^4}=\frac{3}{16}\)
b.
\(\frac{6^3+3\times6^2+3^3}{-13}=\frac{\left(2\times3\right)^3+3\times\left(3\times2\right)^2+3^3}{-13}=\frac{2^3\times3^3+3\times3^2\times2^2+3^3}{-13}=\frac{8\times3^3+3^3\times4+3^3}{-13}\)\(=\frac{3^3\times\left(8+4+1\right)}{-13}=\frac{27\times13}{-13}=-27\)
c.
\(\frac{5^4\times20^4}{25^5\times4^5}=\frac{\left(5\times20\right)^4}{\left(25\times4\right)^5}=\frac{100^4}{100^5}=\frac{1}{100}\)
d.
\(\left(\frac{5^4-5^3}{125^4}\right)=\frac{5^3\times\left(5-1\right)}{\left(5^3\right)^4}=\frac{5^3\times4}{5^{12}}=\frac{4}{5^9}\)
a)\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{2^5.3^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{3}{2^4}\)
b)\(\frac{6^3+3.6^2+3^3}{-13}=\frac{6.6^2+3.6^2+3^3}{-13}=\frac{6^2.\left(6+3\right)+3^3}{-13}=\frac{6^2.9+3^3}{-13}=\frac{6^2.3^2+3.3^2}{-13}=\frac{3^2.\left(6^2+3\right)}{-13}=\frac{3^2.39}{-13}=3^2.\left(-3\right)=-27\)
c)\(\frac{5^4.20^4}{25^5.4^5}=\frac{100^4}{100^5}=\frac{1}{100}\)
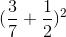 =
= 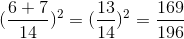
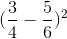 =
= 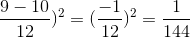
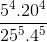 =
= 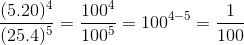
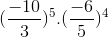 =
= 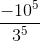 .
. 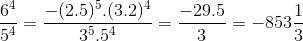


a) \(\dfrac{4^2.4^3}{2^{10}}\)
Hướng dẫn:
- Đưa các lũy thừa trên tử số về cơ số có dạng giống mẫu số
\(=\dfrac{\left(2^2\right)^2.\left(2^2\right)^3}{2^{10}}\)
- Dùng tính chất \(\left(a^n\right)^m=a^{n.m}\) để làm
\(=\dfrac{2^4.2^6}{2^{10}}\)
- Gộp các lũy thừa cùng cơ số lại, dùng tính chất \(a^m.a^n=a^{m+n}\)
\(=\dfrac{2^{10}}{2^{10}}\)
- Chia tử và mẫu cho nhau, dùng tính chất \(a^m:a^n=a^{m-n}\)
\(=1\)
b) \(\dfrac{2^7.9^3}{6^5.8^2}\)
Hướng dẫn:
- Đưa lũy thừa ở tử và mẫu về cơ số nhỏ nhất ( Đưa về cơ số 2 và 3 )
\(=\dfrac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}\)
- Dùng tính chất \(\left(a^m\right)^n=a^{m.n}\) và \(\left(a.b\right)^m=a^m.b^m\)
\(=\dfrac{2^7.3^6}{2^5.3^5.2^6}\)
- Dùng tính chất \(a^m.a^n=a^{m+n}\) để gộp các lũy thừa có cùng cơ số
\(=\dfrac{2^7.3^6}{2^{11}.3^5}\)
- Chia tử và mẫu cho nhau theo cách rút gọn những số giống nhau ở trên tử và mẫu
\(=\dfrac{3}{2^4}\)
\(=\dfrac{3}{16}\)
c) \(\dfrac{5^4.20^4}{25^5.4^5}\)
Hướng dẫn:
- Đưa các lũy thừa của tử và mẫu về cơ số nhỏ nhất ( Cơ số 2 và 5 )
\(=\dfrac{5^4.\left(2^2.5\right)^4}{\left(5^2\right)^5.\left(2^2\right)^5}\)
- Dùng tính chất \(\left(a^m\right)^n=a^{m.n}\) và \(\left(a.b\right)^m=a^m.b^m\)
\(=\dfrac{5^4.\left(2^2\right)^4.5^4}{5^{10}.2^{10}}\)
- Dùng tính chất \(a^m.a^n=a^{m+n}\)
\(=\dfrac{5^8.2^8}{5^{10}.2^{10}}\)
- Rút gọn
\(=\dfrac{1}{5^2.2^2}\)
\(=\dfrac{1}{100}\)