Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TL
Đáp án:
Giải thích các bước giải:a. ta có: N là trung điểm của AC
a. M là trung điểm của BC
=> MN là đường TB của ∆CAB
=> MN // AB => ME//AB
c. AE // BM
AB//EM
=> AEMB là hình bình hành
=> AE=BM=> AE=MC
HT
Lai hộ cái
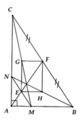
a) ΔABCΔABC cân tại AA mà AMAM là đường cao BCBC
→AM→AM là trung tuyến BCBC (tính chất các đường đồng quy Δ cân)
→M→M là trung điểm BCBC
mà NN là trung điểm ACAC
→MN→MN là đường trung bình ΔABCΔABC
→MN//AB→MN//AB hay ME//ABME//AB
b) Ax//BCAx//BC
→AE//CM→AE//CM
→ˆA1=ˆC1→A1^=C1^ (so le trong)
Xét ΔANEΔANE và ΔCNMΔCNM:
ˆA1=ˆC1(cmt)A1^=C1^(cmt)
AN=CNAN=CN (NN là trung điểm ACAC)
ˆANE=ˆCNMANE^=CNM^ (đối đỉnh)
→ΔANE=ΔCNM(g−c−g)→ΔANE=ΔCNM(g−c−g)
→AE=MC→AE=MC (2 cạnh tương ứng)
c) AMAM là đường cao BCBC
→AM⊥BC→AM⊥BC mà Ax//BCAx//BC
→Ax⊥AM→Ax⊥AM


a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật


a) AC = 10cm Þ SABC =37,5 (cm2)
b) Chứng minh được M A E ^ = A M E ^ (cùng = A B C ^ ) Þ AE = ME. Cmtt ta có AE = NE. Từ đó suy ra ME = NE.
c) Chứng minh EH//GF (//MB) và GE//FH (//NC) Þ EGFH là hình bình hành. Chứng minh được H E G ^ = B A C ^ = 90 0 ⇒ E G F H là hình chữ nhật. Suy ra GH đi qua trung điểm của EF.
S E G F H = H E . E G = 1 2 M B . 1 2 N C = 1 4 . 2 3 A B . 2 3 A C = 25 3 ( c m 2 )
Mà S E G F H = 4. S ⇒ I H F S I H F = 25 12 c m 2