Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
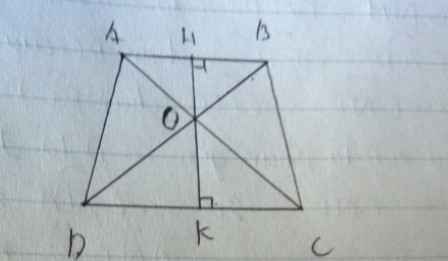
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)

ABssCD⇒ABCD=OBOD=OAOC=23ABssCD⇒ABCD=OBOD=OAOC=23
a)SAOD=12OA.OD.sinAOBSAOD=12OA.OD.sinAOB
SBOC=12OB.OC.sinBOCSBOC=12OB.OC.sinBOC
⇒SAODSBOC=OA.ODOB.OC⇒SAODSBOC=OA.ODOB.OC vì ˆAOD=ˆBOC⇒sinAOD=sinBOCAOD^=BOC^⇒sinAOD=sinBOC
⇔SAODSBOC=23.32=1⇔SAODSBOC=23.32=1
b) vì ABssCD⇒OHOK=23⇒OHHK=25ABssCD⇒OHOK=23⇒OHHK=25
SAOB=12.OH.ABSABCD=12(AB+CD).HK=12(AB+32AB).HK=12.52AB.HKSAOB=12.OH.ABSABCD=12(AB+CD).HK=12(AB+32AB).HK=12.52AB.HK
⇒SAOBSABCD=12OH.AB12HK.52AB=25.152=425⇒SAOBSABCD=12OH.AB12HK.52AB=25.152=425
⇒SABCD=4425=25

<br class="Apple-interchange-newline"><div id="inner-editor"></div>S1,S2,S3,S4lần lượt là diện tích các tam giác AGD,AGB,BGC,CGD
ta có : S1S2 =DGBG =S4S3 ⇒S1.S3=S2.S4(1)
ta thấy tam giác ABD và tam giác ABC có diện tích bằng nhau vì có chung đáy và đường cao không thay đổi.
Mà SABD=S1+S2;SABC=S3+S2⇒S1=S3(2)
Từ (1)và (2)⇒S2.S4=S21⇒S2=S124
⇒SABCD=S1+S2+S3+S4=2S1+S12S4 =2.18+18225 +25=184925 =73,96(cm2)