Câu 5 Thực hiện phép tính: (x-2 phần x+2+6x-4 phần x^2-4 ) :x+1 phần x-2

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PD

Phương Đặng

12 tháng 12 2017

Câu 5

Thực hiện phép tính:

(x-2 phần x+2+6x-4 phần x^2-4 ) :x+1 phần x-2

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

10 tháng 6 2022

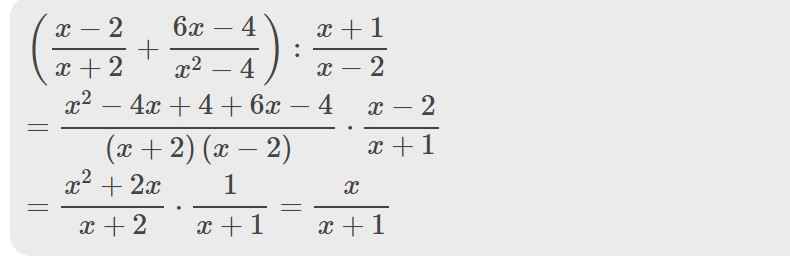
undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

LM

Lê minh quang

25 tháng 3 2020

Tìm x có chứa giá trị tuyệt đối

4|3x-1|+|x|-2|x-5|x-3|=12

2|x+3 1 phần 2|+|x|-3 1 phần 2 = |2 1 phần 5 -x|

#Toán lớp 10

0

PN

Phạm Ngọc Quốc Thắng

13 tháng 2 2020 - olm

Phần 1: Đại sốCâu 1 (2đ): Xét dấu các biểu thức sau:a.f x x     3 4; c.    2f x x x x     1 2 5 2 .b. 2f x x x    9 6 1; d.  22 52xf xx x.Câu 2 (4đ): Giải các bất phương trình sau:a.  23 4 4 0 x x   ; c.  21 2 503x xx .b. 22 4 4 0 x x x   ; d. 225 2 302x xx x.Câu 3 (1đ): Xác định miền nghiệm của bất phương...

#Toán lớp 10

0

TB

Thanh Bình

28 tháng 10 2020

Liệt kê các phần tử của tập A = {x ∈ R|x ² + 4x + 3 = (x+1) √x+5 + √6x+2}

#Toán lớp 10

0

TB

Tam Be

8 tháng 3 2019

Giúp mk giải phương trình lớp8 này ik:

3 phần x-2 trừ 4 phần x+2 bằng 2x^2-4 phần x^2-4

3/×-2 - 4/×+2 =2×^2-4/ ×^2-4

Mk đag vướn bài này mog các bn giúp😊😊

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

8 tháng 3 2019

ĐKXĐ: \(x\ne\pm2\)

\(\frac{3}{x-2}-\frac{4}{x+2}=\frac{2x^2-4}{x^2-4}\)

\(\Leftrightarrow\frac{3\left(x+2\right)}{x^2-4}-\frac{4\left(x-2\right)}{x^2-4}=\frac{2x^2-4}{x^2-4}\)

\(\Leftrightarrow3x+6-4x+8=2x^2-4\)

\(\Leftrightarrow2x^2+x-18=0\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{-1-\sqrt{145}}{4}\\x=\frac{-1+\sqrt{145}}{4}\end{matrix}\right.\)

TB

Tam Be

8 tháng 3 2019

145 từ đâu có vậy bn

DT

đỗ thị loan

9 tháng 12 2019

bài 1 ; thực hiện phép tính

a. ( 2x + 1) . ( x-3)

b. ( x-4) . ( x ^2- 2x +3)

c. ( 2x + 3)^2 - ( 2x-3)^2

d. ( x+4) . (x^2 - 4x +16)

bài 2 phân tích đa thức thành nhân tử

a. x^3 -2x^2+x

b. x^2 - 6x +5

#Toán lớp 10

0

RG

Random Guy On The Internet

23 tháng 6 2020 - olm

Gọi S là tập hợp tất cả giá trị nguyên dương và nhỏ hơn 9 của m để bất phương trình x² + 6x <= 2m( |x + 3| - 2 ) - 6 có nghiệm thực. Tính tổng tất cả các phần tử của S

#Toán lớp 10

0

NT

Nguyễn Thị Lan

12 tháng 4 2020

1)|4-x²|=-3x²+4x+4

2)|x×(x+2)|=|x|

3)|x²-4x-5|=4x-17

4)|x²-6x+5|=x+5

5)|x²-4|+|x|=1

6)|x²-5x-5|=1

#Toán lớp 10

0

CG

Co Gai Ngay Xua

25 tháng 12 2018

1 Thực hiện phép tính

a.(a-b)(a+b)

b.(8^3y^3-12y^3-12x^3y^5):2x^3y^2

c.(x^3+1):(x^2-x+1)

2.phân tích đa thức thành nhân tử

a.6x^2y-18xy^2

b.x^3+x^2-4x-4

#Toán lớp 10

2

AH

Akai Haruma

Giáo viên

25 tháng 12 2018

Bài 1:

a) \((a-b)(a+b)=a^2-b^2\) (theo hằng đẳng thức đáng nhớ)

b) \((8x^3y^3-12y^3-12x^3y^5):(2x^3y^2)=\frac{8x^3y^3}{2x^3y^2}-\frac{12y^3}{2x^3y^2}-\frac{12x^3y^5}{2x^3y^2}\)

\(=4y-\frac{6y}{x^3}-6y^3=4y-6x^{-3}y-6y^3\)

c)

\((x^3+1):(x^2-x+1)=\frac{x^3+1}{x^2-x+1}=\frac{(x+1)(x^2-x+1)}{x^2-x+1}=x+1\)

AH

Akai Haruma

Giáo viên

25 tháng 12 2018

Bài 2:

a)

\(6x^2y-18xy^2=6xy(x-3y)\)

b)

\(x^3+x^2-4x-4=(x^3+x^2)-(4x+4)=x^2(x+1)-4(x+1)\)

\(=(x+1)(x^2-4)=(x+1)(x^2-2^2)=(x+1)(x-2)(x+2)\)

TD

tran duc huy

4 tháng 12 2019

Giải pt sau :

1, \(\sqrt{x+1}+\sqrt{4-x}+\sqrt{\left(x+1\right)\left(4-x\right)}=5\)

2, \(\sqrt{x+4}+\sqrt{x-4}=2x-12+2\sqrt{x^2-16}\)

3, \(\sqrt{x+\sqrt{6x-9}}+\sqrt{x-\sqrt{6x-9}}=\sqrt{6}\)

4, \(\frac{4}{x+\sqrt{x^2+x}}-\frac{1}{x-\sqrt{x^2+x}}=\frac{3}{x}\)

5, \(\sqrt{x^2+x+4}+\sqrt{x^2+x+1}=\sqrt{2x^2+2x+9}\)

#Toán lớp 10

1

NT

Nguyễn Thị Ngọc Thơ

4 tháng 12 2019

1.

ĐK: \(-1\le x\le4\)

Đặt \(\sqrt{x+1}+\sqrt{4-x}=t\left(t\ge0\right)\)

\(\Leftrightarrow\sqrt{\left(x+1\right)\left(4-x\right)}=\frac{t^2-5}{2}\)

\(PT\Leftrightarrow t+\frac{t^2-5}{2}=5\Rightarrow t^2+2t-15=0\) \(\Rightarrow\left[{}\begin{matrix}t=3\\t=-5\left(l\right)\end{matrix}\right.\)

\(t=3\Rightarrow\sqrt{-x^2+3x+4}=2\) \(\Leftrightarrow-x^2+3x+4=4\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\) (tm)

2.

ĐK:\(x\ge4\)

Đặt \(\sqrt{x+4}+\sqrt{x-4}=t\left(t\ge0\right)\)

\(\Rightarrow2\sqrt{x^2-16}=t^2-2x\)

\(PT\Leftrightarrow t=2x-12+t^2-2x\)

\(\Leftrightarrow t^2-t-12=0\Rightarrow\left[{}\begin{matrix}t=4\\t=-3\left(l\right)\end{matrix}\right.\) Giải tiếp như trên.

NT

Nguyễn Thị Ngọc Thơ

5 tháng 12 2019

@tran duc huy Bình phương rồi chuyển vế nha.