K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
NN
0
NB
1
3 tháng 11 2017
a, \(x.\sqrt{\frac{2}{5}}\) = \(\sqrt{x^2}.\sqrt{\frac{2}{5}}\) = \(\sqrt{\frac{x^2.2}{5}}\)
b, \(\left(x-5\right).\sqrt{\frac{x}{25-x^2}}\)= \(\sqrt{\left(x-5\right)^2}\). \(\sqrt{\frac{x}{\left(5-x\right)\left(5+x\right)}}\) = \(\sqrt{\frac{\left(x-5\right)^2.x}{\left(x-5\right)\left(x+5\right)}}\)= \(\sqrt{\frac{x.\left(x-5\right)}{x+5}}\)
c,\(x.\sqrt{\frac{7}{x^2}}\) = \(\sqrt{x^2}\). \(\sqrt{\frac{7}{x^2}}\) = \(\sqrt{\frac{x^2.7}{x^2}}\) = \(\sqrt{7}\)
LH
0
LV
3
HN
13 tháng 8 2021
a, \(x^2-6=x^2-\sqrt{6^2}=\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)\)
b, \(x^2+2\sqrt{3}x+3=x^2+2\sqrt{3}x+\sqrt{3}=\left(x+\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
c, \(x^2-2\sqrt{5}x+5=x^2-2\sqrt{5}x+\sqrt{5}=\left(x-\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)\left(x-\sqrt{5}\right)\)
NH
0
LL
0
15 tháng 11 2018
ta có (x-1)(x-2)(x-3)(x-4)-15=(x-1)(x-4)(x-2)(x-3)-15=\(\left(x^2-5x+4\right)\left(x^2-5x+6\right)-15\)(*)
đặt \(t=x^2-5x+5\)thì pt (*) =\(\left(t-1\right)\left(t+1\right)-15=t^2-1-15\)\(=t^2-16=\left(t+4\right)\left(t-4\right)=\)\(\left(x^2-5x+5+4\right)\left(x^2-5x+5-4\right)=\)\(\left(x^2-5x+9\right)\left(x^2-5x+1\right)\)
NT
2
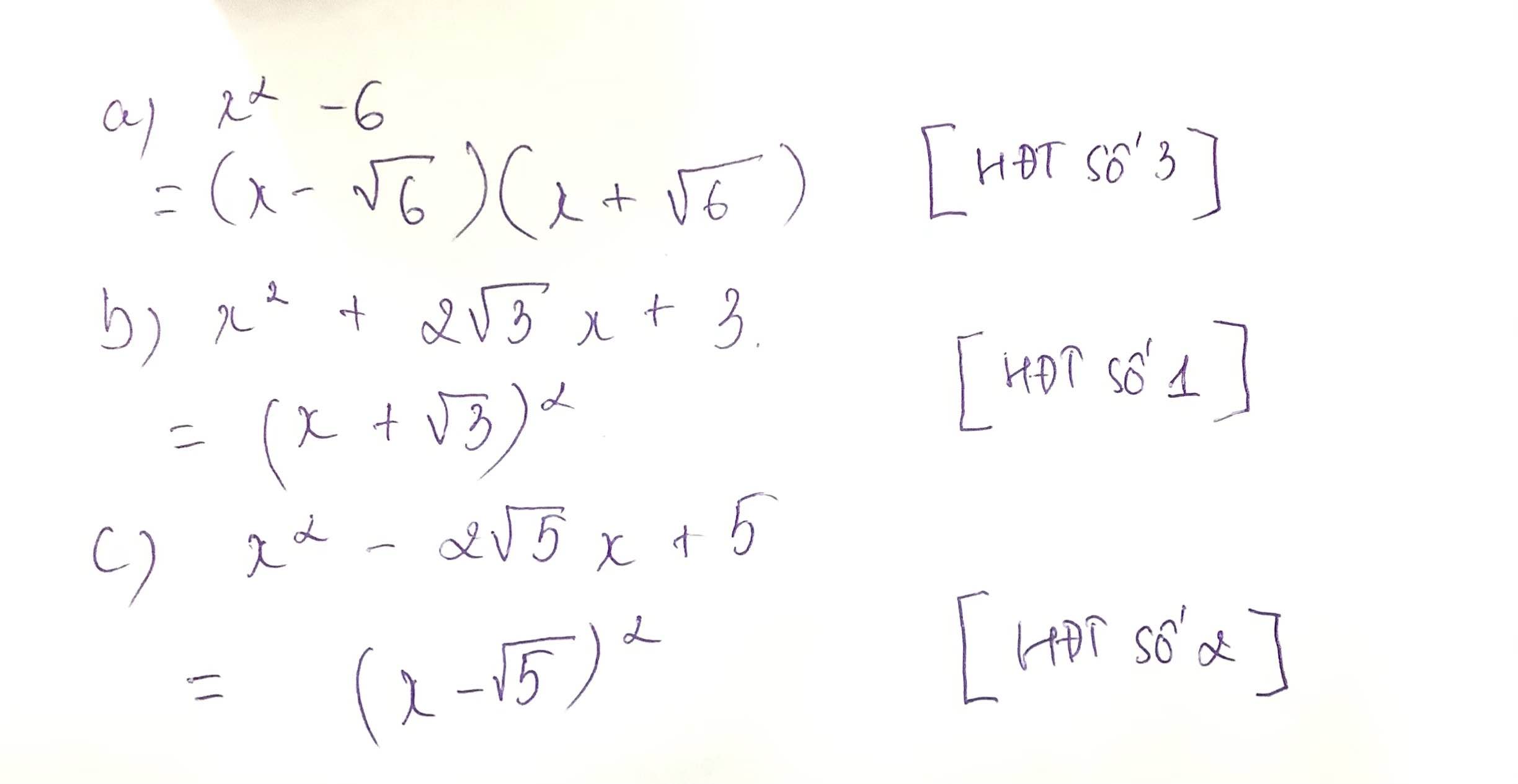
Bài làm
\(3\sqrt{x}=\sqrt{x}+3\Leftrightarrow3\sqrt{x}-\sqrt{x}=3\Leftrightarrow2\sqrt{x}=3\)
\(\Leftrightarrow\sqrt{x}=\frac{3}{2}\Leftrightarrow x=\frac{9}{4}\)
\(3\sqrt{x}=3+\sqrt{x}\)
\(\Leftrightarrow3\sqrt{x}-\sqrt{x}-3=0\)
\(\Leftrightarrow\left(3\sqrt{x}-\sqrt{x}\right)-3=0\)
\(\Leftrightarrow2\sqrt{x}-2=1\)
\(\Leftrightarrow2\left(\sqrt{x}-1\right)=1\)
\(\Leftrightarrow\sqrt{x}-1=\frac{1}{2}\)
\(\Leftrightarrow\sqrt{x}=1+\frac{1}{2}\Leftrightarrow\sqrt{x}=\frac{3}{2}\)
\(\Leftrightarrow x=\left(\frac{3}{2}\right)^2=\frac{9}{4}\)
Vậy \(x=\frac{9}{4}\)
Chúc bạn học tốt