
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm

Có hai trường hợp xảy ra:
Trường hợp 1:
(P) đi qua A, song song với hai đường thẳng d và BC. Vectơ chỉ phương của d là v → (-3; -1; 2) và BC → (-2; 4; 0).
Do đó n P → = v → ∧ BC → = (-8; -4; -14).
Phương trình mặt phẳng (P) là: -8(x - 1) - 4(y - 2) - 14(z - 1) = 0 hay 4x + 2y + 7z - 15 = 0
Trường hợp 2:
(P) đi qua A, đi qua trung điểm F(1; 1; 1) của BC, và song song với d.
Ta có: FA → (0; 1; 0), FA → ∧ v → = (2; 0; 3).
Suy ra phương trình của (P) là: 2(x - 1) + 3(z - 1) = 0 hay 2x + 3z - 5 = 0.

Phép đặt Euler \(\sqrt{x^2+3}=x+t\)
Nói rồi nên không muốn nói lại nữa
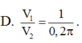
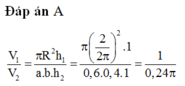
chịu thôi cbos tay
:D đoán đi