Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
ti le 3 canh la 3/4/5 (dinh li pytago)
2 canh goc vuong lan luot la
125 : 5 x 4 = 100
125 : 5 x 3 = 75
hjuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
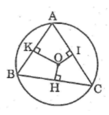
Tam giác ABC có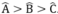 
nên suy ra :
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây lớn hơn gần tâm hơn)
A B C
Áp dụng định lý Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=10\)
\(sinB=\frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}\) \(\Rightarrow\)\(cosC=\frac{4}{5}\)
\(cosB=\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}\) \(\Rightarrow\) \(sinC=\frac{3}{5}\)
\(tanB=\frac{AC}{AB}=\frac{8}{6}=\frac{4}{3}\) \(\Rightarrow\)\(cotC=\frac{4}{3}\)
\(cotB=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}\) \(\Rightarrow\)\(tanC=\frac{3}{4}\)
Cảm ơn nhiều nhé ^^ . mình rất ngu toán . Được bạn giúp thật tốt quá
a:Xét tứ giác BHKC có \(\widehat{BHC}=\widehat{BKC}=90^0\)
nên BHKC là tứ giác nội tiếp
b: Xét đường tròn ngoại tiếp tứ giác BHKC có
\(\widehat{BHC}\) là góc nội tiếp chắn cung BC
\(\widehat{HKB}\) là góc nội tiếp chắn cung HB
mà BC>HB
nên \(\widehat{BHC}>\widehat{HKB}\)