Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Méo thấy hình :D
Cho hình mà chẳng vẽ thì có thánh thần mới làm được.


tập hợp N là số nguyên (1)
mà A = giá tri nguyên (2)
và x < 30 (3)
từ (1),(2),(3) ta có:
x={0;1;2;3;...;29}

TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

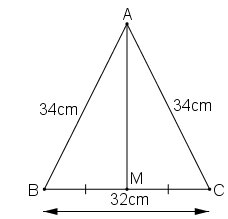
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

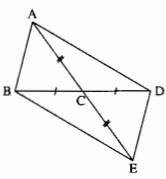
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
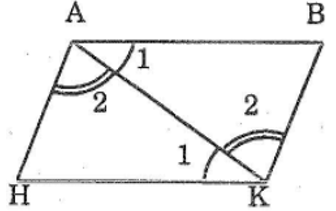
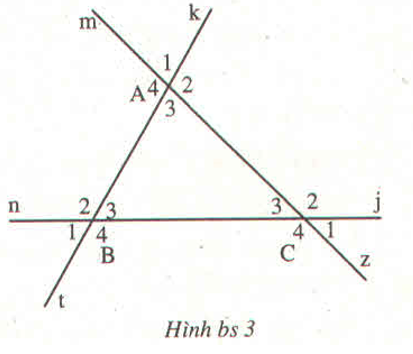
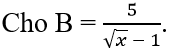
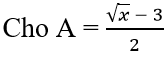

Mình không thể vẽ ra hình đề bài cho được.