Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Bình có 2 khả năng thắng cuộc:
+) Thắng cuộc sau lần quay thứ nhất. Nếu Bình quay vào một trong 5 nấc: 80, 85, 90, 95, 100 thì sẽ thắng nên xác suất thắng cuộc của Bình trường hợp này là P 1 = 5 20 = 1 4
+) Thắng cuộc sau 2 lần quay. Nếu Bình quay lần 1 vào một trong 15 nấc: 5, 10, ..., 75 thì sẽ phải quay thêm lần thứ 2. Ứng với mỗi nấc quay trong lần thứ nhất, Bình cũng có 5 nấc để thắng cuộc trong lần quay thứ 2, vì thế xác suất thắng cuộc của Bình trường hợp này là P 2 = 15 × 5 20 × 20 = 3 16
Từ đó, xác suất thắng cuộc của Bình là
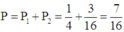

Đáp án D
Xác suất 2 bạn hòa nhau 1 – 0,3 – 0,4 = 0,3.
Để hai bạn dừng chơi sau 2 ván cờ thì ván 1 hòa, ván 2 không hòa
vậy xác suất là 0,3.0,7 = 0,21.

Số học sinh cả lớp là: 2 : 2/48 = 48 học sinh
Số HS nam bằng 3/5 số HS nữ, nên số HS nam bằng 3/8 số HS cả lớp
Khi 10 HS nam chưa vào lớp thì số HS nam bằng 1/7 số HS nữ tức bằng 1/8 số HS cả lớp.
Vậy 10 HS biểu thị 3/8 - 1/8 = 1/4 (HS cả lớp)
Nên số HS cả lớp là: 10 : 1/4= 40 (HS)
Số HS nam là : 40. 3/8 = 15 (HS)
Số HS nữ là : 40. 5/8 = 25 (HS)

Chọn A
Vì mỗi câu có 4 phương án trả lời và chỉ có một phương án đúng nên xác suất để chọn đúng đáp án là 1 4 , xác suất để trả lời sai là 3 4
Gọi là biến cố bạn Nam được trên 8,5 điểm thì A ¯ là biến cố bạn Nam được dưới 8,5 điểm
Vì bạn Nam đã làm chắc chắn đúng 40c âu nên để có A ¯ xảy ra 2 trường hợp
TH1: Bạn Nam chọn được một câu đúng trong 10 câu còn lại, xác suất xảy ra là:
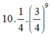
TH2: Bạn Nam chọn được hai câu đúng trong 10 câu còn lại, xác suất xảy ra là:
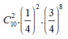
Vậy ![]()
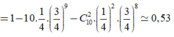

Theo em ý kiến của bạn Nam là đúng.
Ta có: Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne g\left( {{x_0}} \right)\)
Do đó \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) + \mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne f\left( {{x_0}} \right) + g\left( {{x_0}} \right)\)
Vì vậy hàm số không liên tục tại x0.

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
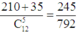

Chọn B.
Không gian mẫu có số phần tử là ![]() .
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: ![]() .
.
Vậy xác suất cần tính là 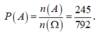 .
.

Đáp án D.
Gọi A:”Bạn được chọn có số thứ tự lớn hơn số thứ tự của Nam”.
